^Motion on a rough inclined plane

^Motion on a rough inclined plane

Consider a body placed on a rough inclined plane.

The y component of the gravitational pull mg cosθ presses the plane & is balanced by normal reaction from the plane, thus N = mg cosθ.

The x component of the gravitational pull mg sinθ (say, F) tends to move the block down the plane, but can do so, only if it exceeds the limiting friction (f_L = m_smg cosθ) on the block.

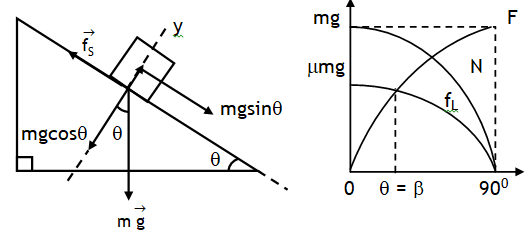
As the inclination θ is increased mgsinθ increases while the limiting frictional force (m_S mg cosθ) decreases. At one stage, mgsinθ & m_S mg cosθ become equal & balance each other then the body placed of the inclined plane at the verge of motion. If the block at this stage is given some velocity it will keep sliding down at constant velocity.

This angle θ is called angle of repose & abbreviated by

symbol β. At θ = β,

or    mg sin θ = m_S mg cosθ

or    tanβ = μ_S

Also we can make following conclusions

1. If θ < β, then F < f_L & block remains at rest. Friction on block is static & equals mg sinθ.
2. If θ = β, then F = f_L & block remains at rest. Friction on block is static & equals mg sinθ or m_smg cosθ.
3. If θ > β, then friction acting on the block is kinetic m_K mg cosθ. This is less than mg sinθ & the block slides down the incline with a uniform acceleration. Using kinematic equations for UAM it can be checked that a block starting from rest will strike the ground with speed in time 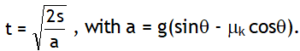This is independent of mass of block.
4. If the inclined plane is smooth (i.e. μ = 0), then the acceleration of a body sliding down a of inclination is, a = g sin θ
5.  Retardation by friction on a rough horizontal surface (i.e. θ = 0⁰) is, a = μ g
6. The force required to move the block up along the inclined plane with const. acceleration a is, F = mgsinθ + μmgcosθ + ma