^Interference of waves

^Interference of waves

Let two waves of amplitudes a₁ & a₂ having a phase difference ΔΦ (or simply Φ) superpose (overlap) at a point P. Let R be the amplitude of the resultant wave, from principle of superposition (POS) R is

As for any wave intensity is proportional to square of its amplitude, i.e.

Let I be the intensity of the resultant wave, then

When the intensity the resultant wave becomes maximum, the situation is called constructive interference (CI), physically it implies crest of one wave exactly overlaps with crest of other & trough with trough, this happens if

Here n = ±1, ±2, ±3, _ _ _ i.e. only integers, n =+ve means above O &– ve below O. Also

When the intensity the resultant wave becomes minimum, the situation is called destructive interference, physically it implies crest of one wave exactly overlaps with trough of other, this happens if

As the value of cosf varies between – 1 to + 1, thus intensity of the resultant wave varies between I_min = (a₁ – a₂)² to I_max = (a₁  + a₂)² so the average intensity is

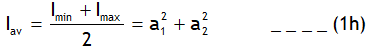
This phenomenon of non-uniform distribution of intensity is called interference of waves.  It is possible for any no. of waves, however for the simplicity we have discussed it for two waves only. Also it is a property of both types of waves, mechanical & EM wave.