*Uniform acceleration
*Uniform acceleration
If in equal intervals of time velocity changes by equal amounts, then the acceleration is called uniform & such a motion is called Uniformly Accelerated Motion (UAM).
1 D Kinematic equations of UAM
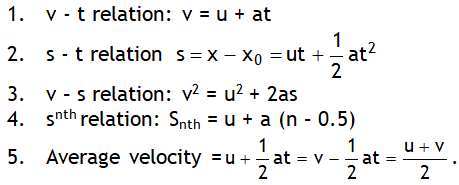
In the above relations S is displacement & not distance.
As in a circular motion & SHM acceleration is not a constant thus these relations are not applicable there. If motion is 2 D or 3 D then kinematics equations are applied either in vector form or separate equations each along x, y & z directions are considered.
Facts
- Magnitude of instantaneous velocity is always equal to instantaneous speed, but magnitude of average velocity is equal to average speed only for uniform motion.
- Zero velocity not necessarily means zero acceleration e.g. if a body stops momentarily under the influence of a retarding force, then at that moment its velocity is zero but its acceleration is equal to net force divided by its mass.
Special situations of UAM
- The two ends of a train moving with a constant acceleration pass a certain point with velocities u and v. Then the velocity of the midpoint of the train when it passes the same point will be RMS of u and v
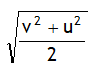(using v – s relation)
2. A boy is standing ‘d’ meters away from a stationary bus. Let the bus begins to move with constant acceleration ‘a’. In order to catch the bus, the boy starts running with a uniform velocity ‘u’ towards the bus as soon as the bus started. Let the boy catches the bus in time t. This is possible only if the total distance travelled by the boy is exactly equal to that travelled by the bus in same time (at2/2).
i.e. d + ut = at2/2
or at2 – 2ut – 2d = 0
In order to catch the bus the roots of above equation must be real, for this the discriminant should not be negative
i.e. (-2u)2 > 4 (-2d) (a) ≥ 0
Simplifying the quadratic time taken by the boy to catch the bus can also be calculated.
3.The driver of a train moving at a speed v1 observes another train at a distance d ahead of him on the same track moving in the same direction with a slower speed v2. He applies the brakes and gives his train constant deceleration a. To prevent collision ‘d’ should be greater than
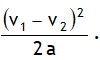
4.If a particle accelerates from rest for time ‘t1’ & covers a distance ‘x1 ‘ at the rate ‘a 1’ & then retards to rest at the rate ‘a2’ over a distance ‘x2’ in time ‘t2’ . Let the maxi. velocity of the particle is Vmax , total distance covered be S and total time spent is t1 + t2 = T (say) as shown in the v – t graph.
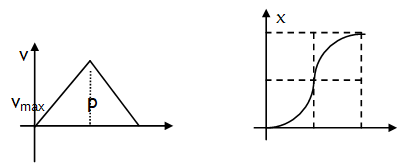
Curved portions in the x – t graph are parabolic.
Using area under v – t graph with t axis is equal to displacement and slope of v – t graph is acceleration we can write,
For portion op
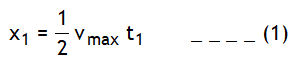
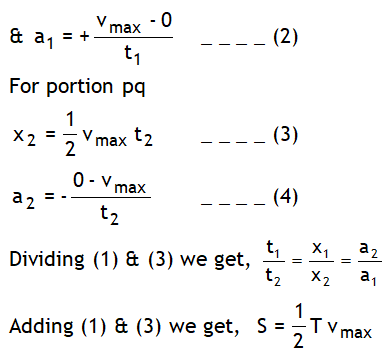
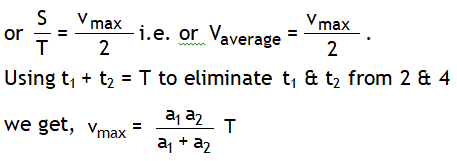
Now the above result to ready to use, don’t put the sign of retardation of a2 again in this relation.
5. The velocity of a train increases at a constant rate a1 from 0 to v in time t1 & covers a distance x1 in this time and then remains constant for time t2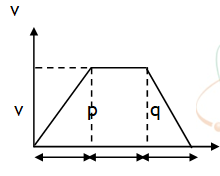 
covers a distance x2 in this time and then finally decrease to zero at a constant rate a3 in time t3 & covers a distance x3 in this time, then we can write
