^Rules of differentiation
^Rules of differentiation
Following table displays some commonly used differentials in physics.
Posts
^Electrostatic force
Electrostatic force
Electrostatic force has following properties
1. Force on any charged particle situated in its electrostatic electric field is given by
[Called electrostatic Lorentz force
2. This force is independent of direction or amount of their velocity.
3. It acts in the direction of field on a positive charge & acts opposite to the direction of field on a negative charge.
4. Acceleration of a charge particle due to force exerted by the electric field using NSL is 
5. Both +ve & -ve charge particle when accelerate under this force always moves in the direction of decreasing potential energy, mathematically this situation is expressed as
Called law of conservative force.
6. Dropping integral & vector sings & rearranging the above relation can be expressed as 
i.e. a conservative force is equal to negative of potential energy gradient.
7. Loss of potential energy of a system implies equal amount of gain in the KE so that the mechanical energy (i.e. K + U) of the system moving in electrostatic electric field is always conserved (i.e. constant). This is why electrostatic force is called conservative.
^Properties of charge
*Properties of charge
1. Charge is scalar, i.e. has no direction.
2. Charge is additive i.e. total charge on a body is given by addition of individual charges for discrete distribution & by integration for continuous distribution.
3. Charge is conserved in any isolated process
4. Charge is quantized i.e. charge smaller than electronic charge, e = 1.6 x 10 – 19 C (also called elementary charge.) is not possible and exists in integral multiple of e i.e. mathematically.
Q = Ne, here N is an integer.
5. Charge is invariant of space, time & velocity.
6. Charge is can’t exist without mass.
*Circle The locus of a point P (x, y) which moves in a plane so that its distance from a fixed point is always a
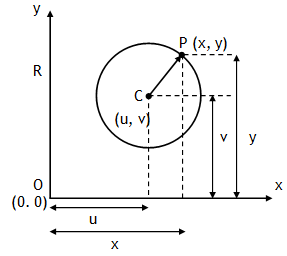
*Circle The locus of a point P (x, y) which moves in a plane so that its distance from a fixed point is always a constant. The fixed point is called the centre C (u, v) of the circle and the constant distance is called its radius (R).
Also a radius of a circle is a straight line joining the centre any point on the circumference. As CP = R, thus using displacement formula we can write
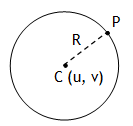
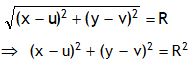
The above expression is called Central form of a circle.
A circle can also be expressed as
ax2 + by2 + 2 gx + 2 fy + c = 0
This expression is called general form of a circle.
Here (-g, -f) is the center of the circle
is radius
If centre of a circle coincides with origin O (0, 0) then the above expression can be written as,
x2 + y2 = R2.
This expression is called Standard form of a circle.
*Intercept form
*Intercept form
Suppose a line cuts x axis at point A (a, 0) and cuts y axis at a point B (0, C), then it can be described by the equation,
[called intercept form].
*Harmonic progression
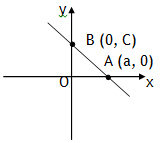
*Harmonic progression
If a, a + d, a + 2d, _ _ _ _ _ _ _ are in AP, then their reciprocals 
are in harmonic progression (HP).
*Logarithms Let a is an arbitrary positive real number except 0. If ax = y, then logay = x
*Logarithms
Let a is an arbitrary positive real number except 0. If ax = y, then logay = x
Conversely, the antilogarithm of x is the number y i.e. y = antilogax.
Here ax = y is called arbitrary exponential function and loga y = x is read is log of y to the base a is equal to x. If a = 10, log is called common & if it is e, then called natural.
*Slope of a straight line
*Slope of a straight line
- Slope (symbol, m) of a straight line is defined as the tan of the anticlock wise angle made by that line with the positive horizontal axis.
- i.e. m = tan θ
- As tan θ can have any real value, so we can say
- Slope of a straight line passing through points A (x1, y1) & B (x2, y2) is given by
- Here Δx, Δy represents change in x & y coordinates respectively.
- If two lines are ||, then their slopes are equal.
- If two lines are perpendicular then the product of their slope is – 1.
*Finding values of θ > 90
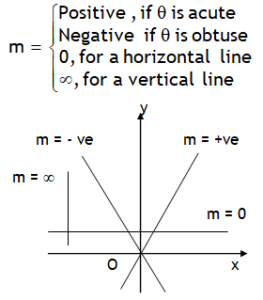
*Finding values of θ > 900
*Expansion formulae sin (A ± B) = sin A cos B ± cos A sin B
*Expansion formulae
sin (A ± B) = sin A cos B ± cos A sin B
cos (A ± B) = cos A cos B ± sin A sin B
