^Lenz rule
^Lenz rule
Induced EMF produced in a circuit always flows in a direction so as to oppose its cause (i.e. change of magnetic flux).
Posts
^Electromagnetic induction
^Electromagnetic induction
Faraday discovered that a time-varying magnetic field produces an electric field more precisely time varying magnetic flux linked with a circuit induces an electric field in it. This field is non conservative & forms closed loops in the circuit in which it is induced (unlike electrostatic electric field, which never forms closed loop & is conservative). Line integral of this electric field gives emf induced (ε) it lasts as long as the change in magnetic flux continues & is defined as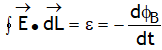 
(Called Faraday flux rule)
This electric field pushes the charges around the circuit, if the circuit is closed & has say resistance R, a current starts flowing in it, given by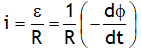 
.
The emf induced is independent of resistance of the circuit but current depends on resistance.
Work done in moving a charge around in induced electric field in a cyclic path is not zero, & W = q ε.
The charge induced doesn’t depend on the rate of change of the magnetic flux, instead is depends on the net change in flux & is 
.
^Commonly used results in electricity & magnetism
^Commonly used results in electricity & magnetism
| Electricity | Magnetism | |
| Source of field | Static or moving charges | Moving charges |
| SI units | Charge: coulomb (C)Electric field: Newton /coulomb (N/C) | Magnetic pole: ampere meter (Am).Magnetic field is tesla (T) |
| Field lines | Discontinuous: Start at a + ve charge & end at equal -ve charge. | Continuous: Have no start or end & are closed loops. |
| Field due to a mono pole |  |
 |
| Proportionality constant |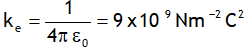 
(SI units) ke = 1 in cgs units |
 in SI unitskm = 1 in cgs units |
| Force on a monopole |  |
 |
| Potential due to a mono pole |  |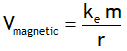
 |
| Coulomb’s law of two point poles |  |
 |
| Screening or shielding | Using hollow metallic boxes. | Using ferromagnetic boxes. |
| Gauss’s law |  |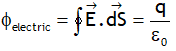
 |
| Force exerted by field on charge particles |  |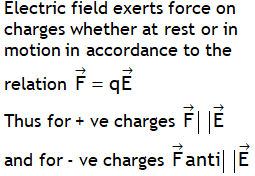
 |
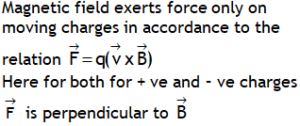| Trajectories of charged particles in field | In electric field:
1. Straight line if the angle between electric field & velocity of the charges particle is 00 or 1800 & 2. parabolic if the angle between electric field & velocity of the charges particle is other than 00 & 1800. |
In magnetic field:
1. Straight line if the angle between magnetic field & velocity of the charges particle is 00 or 1800, 2. circular if the angle between magnetic field & velocity of the charges particle is 900. 3. helical if the angle between magnetic field & velocity of the charges particle is other than 00, 900 & 1800. |
| Dipole moment of a dipole of length 2 L |  |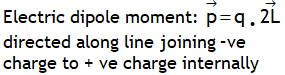
 |
| Field on axial line of a dipole |  |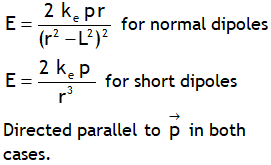
 |
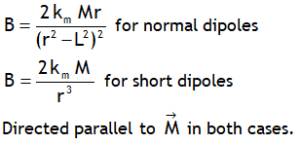| Field on equatorial of a dipole |  |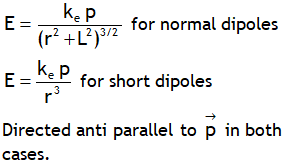
 |
| Field at any point of short dipole |  |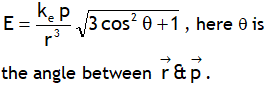
 |
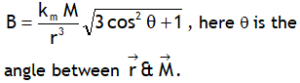| Potential on the axial line of dipole |  |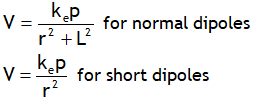
 |
| Potential at any point of short dipole |  |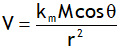
 |
| Force on a dipole placed in a region of uniform field | Force on each pole = qE
Net force on dipole = 0 |
Force on each pole = mB
Net force on dipole = 0 |
| Force on a dipole placed in a non uniform field |  |
 |
| Torque acting on dipole placed in a region of uniform field |  |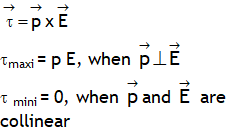
 |
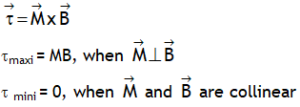| Condition for equilibrium of dipole placed in a region of uniform field |  |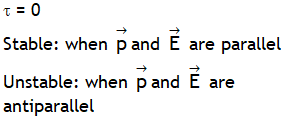
 |
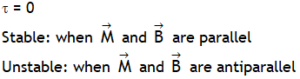| Potential energy of dipole – field system placed in a region of uniform field |  |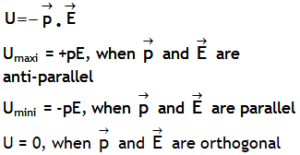
 |
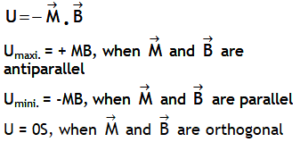^Tangent galvanometer
^Tangent galvanometer
It is an instrument used to detect small currents using tangent law by keeping the magnetic needle at equilibrium under the torques of the Bcoil & BH.
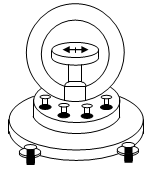
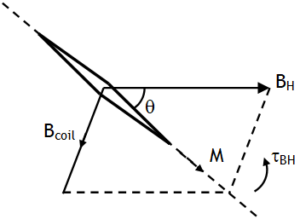
The plane of the coil is set parallel to the magnetic meridian such that the magnetic needle points 0– 0 position. Now current to be measured is passed in the coil. The magnetic field produced by this current acts at right angles to the plane of the coil. Torque due to this field deflects the needle while the torque due to BH tends to restore the needle till the equilibrium is achieved. Let in equilibrium the magnetic needle makes an angle θ with the horizontal component of earth’s magnetic field, then we can write
Bcoil = BH tanθ
or I = k tanθ
Here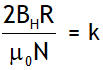 
is called reduction factor.
It is the amount of current required to produce a deflection of 450 in the magnetic needle. A tangent galvanometer is said to be both sensitive & accurate, if the change in its deflection is large for a given fractional change in current. The percentage error in the measurement of current is minimum when the deflection is 450.
^Dip (δ) & Horizontal component
^Dip (δ) & Horizontal component
The vertical component of the Earth’s magnetic field points downwards in the northern hemisphere. If the magnetic needle of a dip circle is perfectly balanced about a horizontal axis so that it dips (moves down) in a vertical plane of the magnetic meridian and aligns. Itself at some angle to horizontal at which 
are parallel, this angle is known as the angle of dip (also known as inclination).
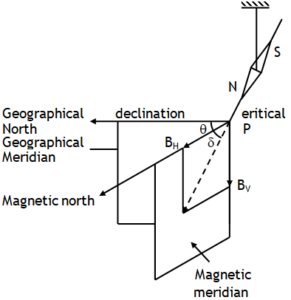
We can say that angle of dip at a place in the magnetic meridian is the angle between horizontal component of earth’s magnetic field (H) & its resultant intensity (B) or it is the angle made by the axis of a freely suspended magnet with the horizontal line. e.g. Dip angle = 420 at Delhi.
In figure shown, the resultant magnetic field is in the magnetic meridian, d is angle of dip, BH and BV denote horizontal and vertical components of Earth’s magnetic field respectively.
BH = B cosδ, BV = Bsinδ
Exactly at the equator the Earth’s magnetic field is parallel to the Earth’s surface, angle of dip & vertical component of Earth’s magnetic field are zero, thus a freely suspended magnet will be horizontal at the equator. Exactly at the centre of poles the Earth’s magnetic field is normal to the surface of the Earth, angle of dip is 900 and the horizontal component of the Earth’s magnetic field is zero. Therefore a freely suspended magnet will become vertical at the poles.
^Dipole’s natural alignment
Dipole’s natural alignment
Any magnetic needle (or a dipole) free to move in a region of external magnetic field aligns so that its dipole moment become parallel to external magnetic field i.e. 
i.e. the position of stable equilibrium. This is because the position of stable equilibrium is the position of maximum stability or minimum potential energy.
^Superconductors: Perfect diamagnetics
Superconductors: Perfect diamagnetics
For super conductors cooled to very low temperatures χ = –1 & μr = 0.
Thus the super conductors are perfect diamagnetic materials. The phenomenon of perfect diamagnetism in superconductors is calledthe Meissner effect. In superconductors the field lines are completely expelled. Also a superconductor repels a magnet and (by Newton’s third law) is repelled by the magnet.
Superconducting magnets can be used in variety of situations, for example, for running magnetically levitated super fast trains.
Magnetic lines prefer to pass through air than through a diamagnetic material & through a ferromagnetic material than through air.
^Some more useful situations
Some more useful situations
1. The ratio of magnetic dipole moment to angular momentum for a uniformly charged configuration 
2. A current loop behaves like a magnetic of dipole moment M = A N I, here I → current in loop, A → loop area & N → its no. of turns.
3. A current loop placed of dipole moment 
in external uniform magnetic field 
experiences a torque, 
.
4. A current carrying conductor placed in uniform magnetic field experiences a force. 
5. For a closed loop of any shape net force on it is zero, however depending upon direction of current & external magnetic field a tension T = RBI may produce.
6. Two straight parallel conductors experience a force 
per unit of their length due to the magnetic field of each other.
^Oersted observation
Oersted observation
Oersted (1820) was the first to discover magnetic field associated with a current carrying conductor. He found that if a wire carrying a current from South to North is placed Over a magnetic needle, then the north pole the needle gets deflected towards the West. This is named as SNOW rule.
*Uniform acceleration
*Uniform acceleration
If in equal intervals of time velocity changes by equal amounts, then the acceleration is called uniform & such a motion is called Uniformly Accelerated Motion (UAM).
1 D Kinematic equations of UAM
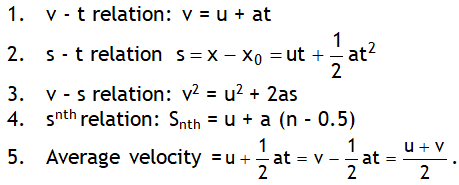
In the above relations S is displacement & not distance.
As in a circular motion & SHM acceleration is not a constant thus these relations are not applicable there. If motion is 2 D or 3 D then kinematics equations are applied either in vector form or separate equations each along x, y & z directions are considered.
Facts
- Magnitude of instantaneous velocity is always equal to instantaneous speed, but magnitude of average velocity is equal to average speed only for uniform motion.
- Zero velocity not necessarily means zero acceleration e.g. if a body stops momentarily under the influence of a retarding force, then at that moment its velocity is zero but its acceleration is equal to net force divided by its mass.
Special situations of UAM
- The two ends of a train moving with a constant acceleration pass a certain point with velocities u and v. Then the velocity of the midpoint of the train when it passes the same point will be RMS of u and v
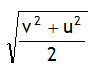(using v – s relation)
2. A boy is standing ‘d’ meters away from a stationary bus. Let the bus begins to move with constant acceleration ‘a’. In order to catch the bus, the boy starts running with a uniform velocity ‘u’ towards the bus as soon as the bus started. Let the boy catches the bus in time t. This is possible only if the total distance travelled by the boy is exactly equal to that travelled by the bus in same time (at2/2).
i.e. d + ut = at2/2
or at2 – 2ut – 2d = 0
In order to catch the bus the roots of above equation must be real, for this the discriminant should not be negative
i.e. (-2u)2 > 4 (-2d) (a) ≥ 0
Simplifying the quadratic time taken by the boy to catch the bus can also be calculated.
3.The driver of a train moving at a speed v1 observes another train at a distance d ahead of him on the same track moving in the same direction with a slower speed v2. He applies the brakes and gives his train constant deceleration a. To prevent collision ‘d’ should be greater than
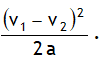
4.If a particle accelerates from rest for time ‘t1’ & covers a distance ‘x1 ‘ at the rate ‘a 1’ & then retards to rest at the rate ‘a2’ over a distance ‘x2’ in time ‘t2’ . Let the maxi. velocity of the particle is Vmax , total distance covered be S and total time spent is t1 + t2 = T (say) as shown in the v – t graph.
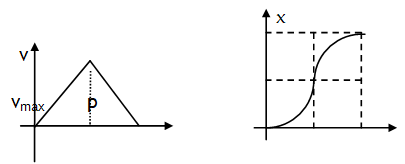
Curved portions in the x – t graph are parabolic.
Using area under v – t graph with t axis is equal to displacement and slope of v – t graph is acceleration we can write,
For portion op
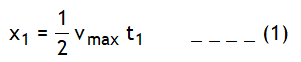
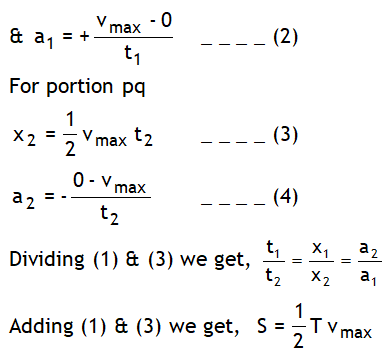
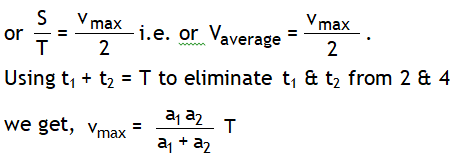
Now the above result to ready to use, don’t put the sign of retardation of a2 again in this relation.
5. The velocity of a train increases at a constant rate a1 from 0 to v in time t1 & covers a distance x1 in this time and then remains constant for time t2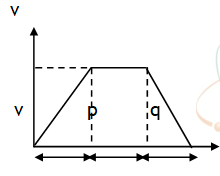 
covers a distance x2 in this time and then finally decrease to zero at a constant rate a3 in time t3 & covers a distance x3 in this time, then we can write
