^Uses of plane mirror
^Uses of plane mirror
- As looking glass
- To bend the path of light
- As periscope
- As Kaleidoscope
Posts
^Image by concave mirror
^Image by concave mirror
As an object approaches the pole of a concave mirror, the size of the image increases, also any kind of image viz. real, virtual, magnified, diminished & of same size is possible. Following is the summary of the various cases of image formation.
1. When an object is placed at ∞, a real, inverted, extremely diminished image is produced at F.
i.e. for u = ∞, v = f & m < < 1
2. When an object is placed beyond C a real, inverted, diminished image is produced between F & C.
i.e. for ∞ > u > 2 f, f < v < 2 f & m < 1
3. When an object is placed at C a real, inverted, image having size same as size that of object is produced between F & C.
i.e. for u = 2 f, v = 2 f & m = 1
4. When an object is placed between F & C, a real, inverted, magnified image is produced beyond C.
i.e. for 2 f > u > f, ∞ > v > 2 f & m > 1
5. When an object is placed at F, a real, inverted, magnified image of infinite size is produced at ∞.
i.e. for u = f , v = ∞ & m → ∞.
6. When an object is placed between F & P, a virtual, erect, magnified image of infinite size is produced beyond 2 F on the other side of mirror.
i.e. for f > u > 0, ∞ > v > 0 & m > 1
Using the image formation rules along with the sign conventions we can explain the various cases of image formation.
^Multiple images
^Multiple images
If two plane mirrors are inclined at an angle θ, then the total no. of images (n) formed by successive reflections at the two mirrors can be calculated directly by using the following approach.
First find the value of m. Here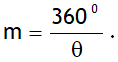 
Then check for the following three possibilities:
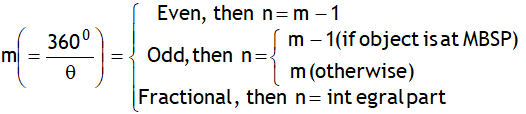
MBSP means mirrors bisector position.
^Newton’s formula
^Newton’s formula
Let x1 & x2 respectively be the distance of object & image from focus instead of from the pole of a mirror or lens, then x1 x2 = f2.
^Mathematical relations for lenses
^Mathematical relations for lenses
^Mathematical relations for mirrors
^Mathematical relations for mirrors
^Sign conventions
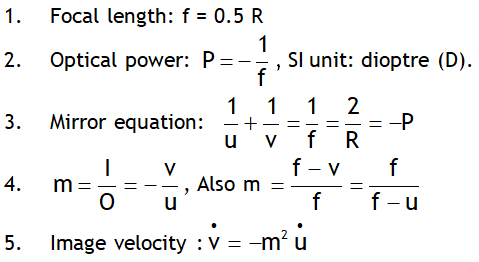
^Sign conventions
Following are the sign conventions for all types of mirrors, lenses, spherical refracting surfaces
1. All distances are measured from the pole of the mirror.
2. Distances measured in the direction of incident ray are +ve & that measured in the opposite direction are –
3. Distances measured upward to the principle axis are +ve & that measured downward are –
Using the image formation rules, sign conventions & simple laws of geometry we can prove the relation between u, v, f, m, I, O, f, R & P.
Don’t put the sign for the quantity to be calculated.
^Divergent power
^Divergent power
1. Bends the reflected (or refracted) rays away from the principal axis
2. Has negative optical power
3. e.g. a convex mirror & a concave lens (placed in rarer surroundings)
^Convergent power
^Convergent power
1. Bends the reflected (or refracted) rays towards the principal axis
2. Has positive optical power
3. e.g. a concave mirror & a convex lens (placed in rarer surroundings)
4. our eyes
5. Used in compound microscope, telescopes, cameras.
^Magnified image
^Magnified image
- I > O
- v > u
- m > 1
Inequality sign reverses for diminished image
