*Integral calculus

*Integral calculus

Integration is the reverse process of differentiation, thus also called anti-differentiation.

Suppose we have a function g (x) whose derivative.

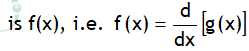
The function g (x) is known as the indefinite Integral of f (x) and is denoted as:

1/d is usually abbreviated by the symbol ∫ (called integral), so one can write

∫ f (x) dx = g (x) + c

Here c is called constant of integration. Its value is arbitrary and can be calculated form the information given in the problem.

Integral of the form 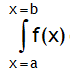    is called definite integral. Here x = a & x = b are called limits of integration. x = a is called lower limit & x = b is called upper limit. If limits are not given, then the integration is called indefinite integration.

Definite integral is a number. Indefinite integral has no limits; it is a function. No integration constant is required in the final answer in definite integrals. Following examples explain how one can derive integration from differentiation.