^Apparent dip

^Apparent dip

Let respectively be the vertical component, horizontal component & dip angle in a vertical plane inclined at some angle say α to magnetic meridian, then .

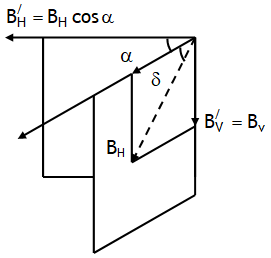
On dividing we wet tanδ^/ = tanδ secα

From above relation we can write

• As sec α > 1, thus for any vertical plane inclined at some angle say α to magnetic meridian dip angle is greater than its value in magnetic meridian i.e. δ^/ > δ.
• δ^/ = 90⁰ if α = 90⁰e. in a plane perpendicular to magnetic meriadian dip needle will be vertical.

In a similar way it can be proved that if δ₁ and δ₂ be the angles of dip observed in two vertical planes at right angles to each other and δ is the true angle of dip, then cot² δ₁ + cot² δ₂ = cot² δ.