^Weight in a lift

^Weight in a lift

Consider a person 1 of mass m (true weight, mg) standing on a weighing scale placed on the floor of a lift. The reading (R) of weighing scale is called his apparent weight, the scale by the person.

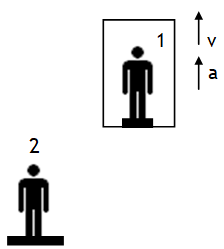
Let the lift is speeding up with acceleration ‘a’ w.r.t.  a stationary ground observer 2 (inertial). Using NSL from the frame of reference of 2 we get:

N – mg = ma                      _ _ _ _ (1)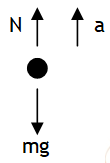   

 

Person 1 is in a non inertial frame, thus experiences a pseudo force (ma) opposite to acceleration of lift frame & is stationary w.r.t. lift under the influence of mg, N & ma, thus

(-mg) + (+N) + (-ma) =0                 _ _ _ _ (2)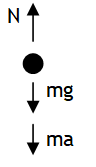   

From (1) & (2) we are getting same result

N = R = m (g + a).

1.       R = m (g + a), if the lift moves

(a)      upward with uniform acceleration or

(b)      downward with uniform deceleration.

2.       R = m (g – a), if the lift moves

(a)      upward with uniform deceleration or

(b)      downward with uniform  acceleration.

3.       R = m g, if the lift moves

(a)      upwards with constant velocity or

(b)      downwards with constant velocity or

(c)      if the lift is at rest.

4.       R = 0, if the lift falls freely under gravity i.e. (a = g).