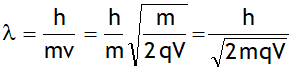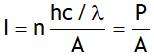^Einstein’s mass-energy equivalence
The relation

is called relativistic energy or Einstein’s mass-energy equivalence as it reveals that mass & energy are interconvertible. Here the quantity m0 c2 is the energy associated with the rest mass of the body, K is the kinetic energy of the body & the sum of KE & rest mass energy is called the total energy (E) of the body.

Differentiating this relation we get
c2.2 m dm – m2.2v dv – v2.2m dm = 0
or c2 dm = mv.dv + v2 dm _ _ _ _ (1)
Also according to Newton’s second law of motion, force acting on a body is defined as the rate of change of its momentum i.e.
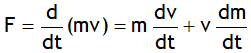
Now if this force F displaces the body by a distance dx, its energy increases by

Equating (1) & (2) we get
dK = dm.c2 _ _ _ _ (3)
If particle is accelerated from rest to a velocity v, let its mass m0 increase to m, then its total increase in KE can be obtained by integrating equation (3) , i.e.
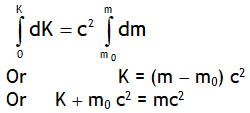
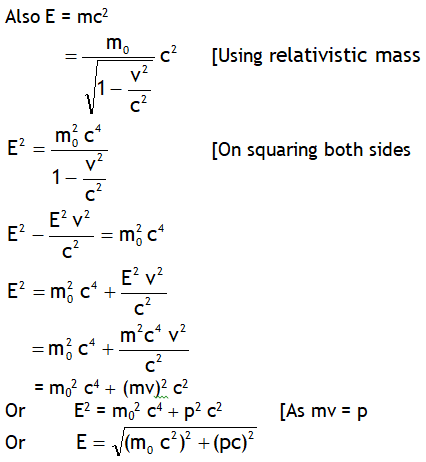
Suppose a body of rest mass m0 moves with a velocity v << c. Its mass at speed v is

As mc2 is the total energy and m0 c2 is the rest mass energy. Therefore the term (mc2 – m0 c2) represents the kinetic energy, thus KE of the body is 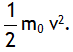
This is the same result that we obtain by classical Newtonian mechanics.
Facts
1. Zero rest mass i.e. m0 = 0 means massless particle & for such particles, E = pc i.e. even a massless particle can possess energy.
2. An electron and photon have same de-broglie wavelength. Which has more total energy?
Ans. Same λ means same p (as, p = h/λ) & quantity having more m0 will have more E, i.e. Electron.
3. An electron and proton have same total energy. Which has more de-broglie wavelength?
Ans. In order to have same E the quantity having less m0 must have more p or less λ (as, p = h/λ), i.e. Electron.
4. Also KE of a particle is
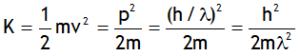
5. If a photon and electron has same de Broglie wavelength, then the KE of the photon is  times the kinetic energy of the electron.
times the kinetic energy of the electron.
Commonly used values
1. Charge of electrons = e = – 1.6 x 10-19 C
2. Rest mass of electrons = m0 = 9.1 x 10-31
3. Sp. charge of electron = e/m0 = 1.76 x 1011 C/ kg
4. hc = 1.989 x 10-25 » 2 x 10-25
5. 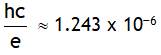


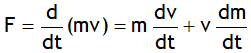

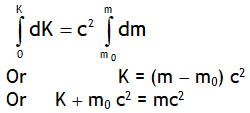
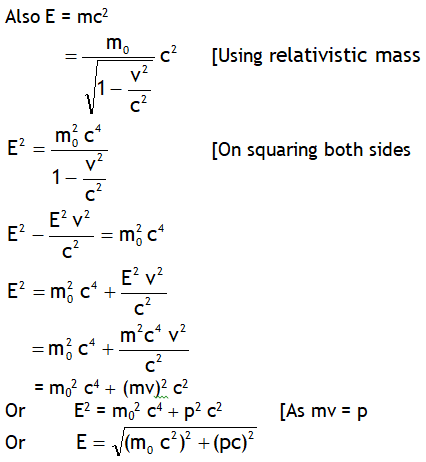

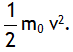
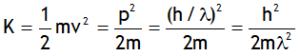
 times the kinetic energy of the electron.
times the kinetic energy of the electron.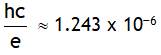
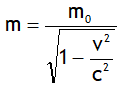
 .
.