^ best physics teacher online for neet - KP Physics

^Rules for writing units

December 23, 2021/in Back end /by kp-web-admin

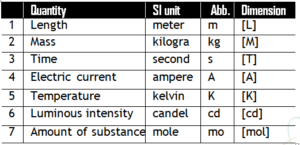
^Rules for writing units

The initial letter of a unit symbol named after a scientist is written in capital letters, however the full name begins with small letter. e.g. five newtons should be written as 5 N or 5 newtons but not as 5 n.
Symbols for various units are never used in plural form. e.g. 5 N should be written as 5 N and not as 5 Ns, however we can write 5 newtons but not 5 Newtons.
Symbols are never followed by a full stop.
Not more than one solidus is used. e.g. Nm^{– 2}s^{– 1}shouldn’t be written as N/m²/s.
The use of double prefix is avoided, when single prefix is available. e.g. instead of writing μμN we should write pN.

In calculations the prefix is attached with the numerator and not with the denominator.

*The Seven Fundamental Quantities

December 23, 2021/in Back end /by kp-web-admin

*The Seven Fundamental Quantities

^Gaussian surface

December 23, 2021/in Back end /by kp-web-admin

Gaussian surface

To find electric field due to a charge configuration using Gauss’s law we draw an imaginary closed surface around that charged distribution.
Gaussian surfaces are normal to electric lines of & symmetric to the charge enclosed such that electric field at every point of the Gaussian surface due to that charged distribution is same.
Gaussian surfaces are spherical for point charges or spherical distribution of charges & cylindrical for linear and planar distribution of charge.
Only those charges which lie inside the Gaussian surface are considered & that located outside have no contribution in the flux.
Discrete charges on the surface of the -Gaussian surface are not considered (as electric field at the location of a discrete charge is not defined) but continuous charges can be considered.

^For infinite line charge

December 23, 2021/in Back end /by kp-web-admin

For infinite line charge

Both α & β will approach to 90⁰ & E becomes

*Integral calculus

December 23, 2021/in Back end /by kp-web-admin

*Integral calculus

Integration is the reverse process of differentiation, thus also called anti-differentiation.

Suppose we have a function g (x) whose derivative.

The function g (x) is known as the indefinite Integral of f (x) and is denoted as:

1/d is usually abbreviated by the symbol ∫ (called integral), so one can write

∫ f (x) dx = g (x) + c

Here c is called constant of integration. Its value is arbitrary and can be calculated form the information given in the problem.

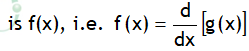
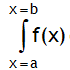Integral of the form is called definite integral. Here x = a & x = b are called limits of integration. x = a is called lower limit & x = b is called upper limit. If limits are not given, then the integration is called indefinite integration.

Definite integral is a number. Indefinite integral has no limits; it is a function. No integration constant is required in the final answer in definite integrals. Following examples explain how one can derive integration from differentiation.