^Inclined plane projectiles
^Inclined plane projectiles
Posts
^Projectile thrown straight up
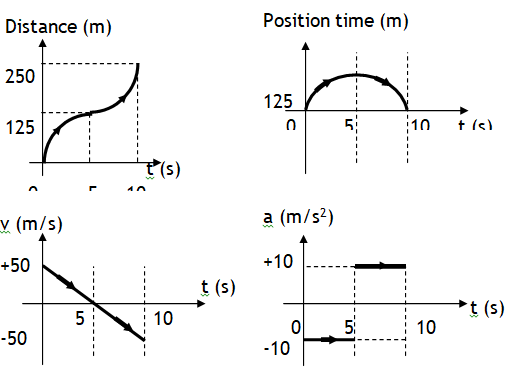
^Projectile thrown straight up
Suppose a body is projected upwards from the ground and with the velocity u. The characteristics of motion of such a body are as follows.
- The maximum height attained
- Time taken to go up (ascent) = Time taken to come down (descent)
- Time of flight
- For an object thrown straight upwards with u = 50 m/s\
- The speed of the body on return to the ground = speed with which it was thrown upwards
- When the height attained is not large, that is u is not large, the mass, the weight as well as the acceleration remain constant with time its speed, velocity, momentum, potential energy and kinetic energy change with time.
-
- Let m be the mass of the body. Then in going from the ground to the highest point, following changes take place.
- Change in speed = u
- Change in velocity = u
- Change in momentum = m u
Change in KE = Change in PE =
-
- On return to the ground the changes in these quantities are as follows:
- Change in speed = 0
- Change in velocity = 2 u
- Change in momentum = 2 mu
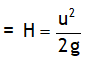
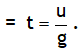
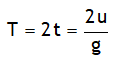
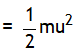
Change in KE = Change in PE = 0
-
- If the friction of air be taken into account, then the motion of the object thrown upwards will have the following properties:
- Time taken to go up (ascent) < time
taken to come down (descent)
- The speed of the object on return to the
ground is less than the initial speed. Same is true for velocity (magnitude), momentum (magnitude) and KE.
- Maxi height attained is less than
. - A part of the KE is used up in overcoming
the friction.
^Relative velocity
^Relative velocity
Concept of relative velocity is required when some moving body is to be observed by a moving observer. Relative velocity A with respect to B means velocity of A as seen by B, & it is defined as,
^Brewster’s law
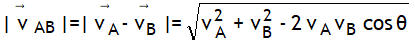
^Brewster’s law
Brewster discovered that when ordinary light is incident on the surface of a transparent medium the reflected light is partially plane polarized.
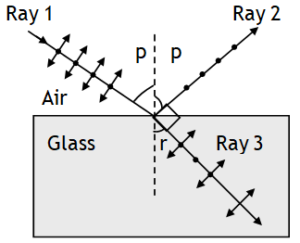
The extent of polarization depends on the angle of incidence. For a particular angle of incidence (called polarizing or Brewster angle (ip or p)
1. the reflected light is found to be completely polarized with its vibrations perpendicular to the plane of incidence.
2. the reflected & transmitted rays are perpendicular to each other, as shown in figure.
3. μ = tan p [called Brewster law
At i = p Ray 1: Incident ray (unpolarised)
Ray 2: Reflected ray (completely polarised)
Ray 3: Refracted ray (partially polarised)
For a ray incident form air to glass
aμg = 3/2, so p = tan-1 3/2 ⇒ p = 56.30
For a ray incident form air to water
aμw = 4/3, so p = tan-1 4/3 ⇒ p = 53.10
^Malus law
^Malus law
Let I0 be the intensity and ‘A’ the amplitude of the unpolarized light falling on the polarizer & θ be the angle between the pass axis of the polaroid & amplitude vector, then the component Acosθ, parallel to the pass axis (y) of polarizer passes through it & the component Asinθ, perpendicular to pass axis is blocked by the polarizer, thus the intensity of light transmitted by the polarizer is
I = k (A cosθ)2 = k A2 cos2 θ
or I = I0 cos2 θ [called Malus law
Actually the phase angle for a beam of unpolarised light can have any value from 00 to 3600. Now as the average value of cos2 θ for the range 00 to 3600 is 0.5, thus the average intensity of light transmitted by a polarizer is only 0.5 I0. Following observations can be explained on the basis of Malus law.
1. Two polarizes with parallel pass axis (y & y)
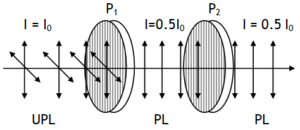
2. Two polarizes with crossed pass axis (y & z)
^Light through a polarizer
^Light through a polarizer
Let ordinary light propagating along +x axis falls normally on a tourmaline crystal having pass axis parallel to y axis as shown in the following diagram. On passing through the tourmaline crystal the electric field vibration parallel to pass axis are transmitted while the electric field vibration normal to pass axis are absorbed by the tourmaline.
^How do polarisers work
^How do polarisers work
A Polaroid is a thin commercial sheet containing long chain of hydrocarbons which become conducting at optical frequencies & absorb the electric field parallel to chains & transmit the electric field perpendicular to the chain length. This is why a direction perpendicular to the chain length is called the transmission axis or pass axis of the polarizer. For shown drawing y axis is pass axis.
^Polarisers
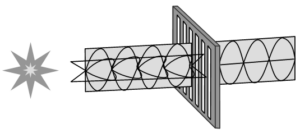
^Polarisers
Any device or material that plane polarizes the unpolarised light passed through it is called a polarizer. Nicol prism, Tourmaline crystal, Polaroid etc. are some commonly used Polarisers.
^Plane polarized light
^Plane polarized light
If the electric field vector of a light wave vibrates just in one direction perpendicular to the direction of wave propagation, then it is said to be linearly polarized along that direction. Human eyes can’t distinguish between an unpolarised light and a polarized light, but the eyes of a bee can.
^Ordinary or unpolarized light
^Ordinary or unpolarized light
Light is made up of the superposition of a huge number of light waves emitted by individual atoms whose electric fields are in random directions. As a result the direction of vibration (DOV) of electric field vector at any given point of space keeps on changing very rapidly & randomly but always remain perpendicular to the direction of propagation (DOP). Such a light is called randomly polarized or simply unpolarized light. If a light wave propagates along x axis then tip of the electric field vector traces an irregular planar curve & there can be infinite directions of vibrations of electric field vector in the yz plane as shown in the diagram.
Light from a light bulb, candle, Sun is unpolarized. Usually we represent electric field vibrations in a ordinary light by dots & double arrows. Here double arrows represent the vibrations in the plane of paper (let xy plane) i.e. along ± y – axis and small dots represent vibrations perpendicular to the plane of paper along i.e. ± z – axis.
