Posts
^Near point case
^Near point case
It the object is placed between F & P of a convex lens such that the images at near point (25 cm) is formed as shown,
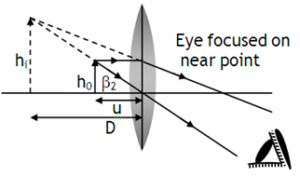
then the magnifying power of lens is 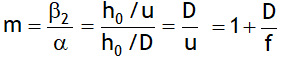
Magnifying power of a simple microscope can be increased by decreasing the focal length of the lens, however generally it is not preferred, as then spherical & chromatic both defects becomes more pronounced. Also it is difficult to grind lenses of very short focal lengths. Consequently a simple microscope has a limited maximum magnification (≤ 9) for realistic focal lengths. For much larger magnifications, one uses two lenses, one compounding the effect of the other.
^Simple microscope
^Simple microscope
A simple microscope is simply a converging lens of small focal length (f < D).

Suppose a short object has a height h0 is viewed by eye without using a lens by pacing it at near point, then the visual angle made by the object eye is

Far point case
It the object is placed at F of a conves lens such that the images at far point (∞) is formed as shown,

then the magnifying power of lens 
^Spherical Aberration
^Spherical Aberration
Due to curvature of a lens marginal rays meet at a point situated at a nearer distance from lens & paraxial rays undergo minimum & meet at a point situated at greater distance for optical center of the lens resulting in a large no. of blurred images. It can never be eliminated but can be minimized
1. Using stops: By using stops either paraxial or marginal rays are cut off, bringing the rest practically to one focus.
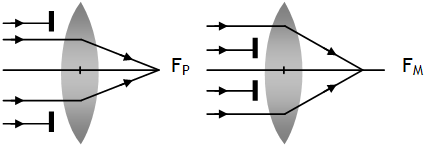
However, in this method, intensity of image formed is poor.
2. Using lens of large focal length
3. Using plano-convex lens such that its curved surface faces the incident or emergent light whichever is more parallel.
^Chromatic aberration
^Chromatic aberration
(a) Various colors in white light get dispersed at various points on the principal axis resulting in a large no. of blurred images.
(b) Longitudinal chromatic abb. = fR – fV =df = – ωf
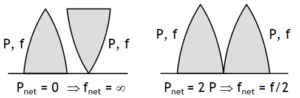
(c) For a combination of two lenses separated by a distance x to produce achromatism.
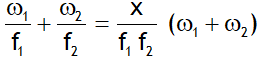
If lenses are in contact, then x = 0 & condition of achromatism becomes.
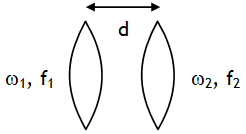
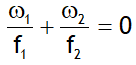
This is possible only if one is convex & other is concave. Also this implies ω ∝ f. In order to produce a convergent achromatic beam from a combination of a convex & concave lens in contact the lens having more focal length must have more dispersive power (more refractive index).
^Polishing lenses
^Polishing lenses
When a mirror is polished it becomes a mirror of focal length ‘f’ given by 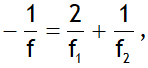
Here f1 & f2 are the focal lengths of surfaces where a ray of light strikes for 1st & 2nd time respectively. As the ray of light strikes the 1st surface twice, hence its contribution is considered twice.
^Displacement method
^Displacement method
This method is used in the labs to find the focal length of a convex lens.

Consider an object placed between a thin convex lens of focal length ‘f’ & a screen at a distance ‘D’ from the screen.
Using Lens formula for this problem one can write:


To get two distinct images the discriminate > 0.

Thus the essential condition to get two distinct real images on the screen is D > 4 f.
From eqn. (1) the two roots of the quadratic i.e. two different distance of the lens from the object are given by:

From these relations the distance between the two positions of the lens (say ‘x’) can be written as:

The image distance can be written as:

This implies that for the two positions of the lens the image & object distances are interchangeable.
The magnification of the two images can be given by:

^Cutting a lens
^Cutting a lens
(a) If a lens of focal length f is given a longitudinal cut (along aperture) into two equal halves as shown in fig. then the focal length of each half becomes 2f.
![]()
(b) If the lens is given a transverse cut (at right angles to aperture) into two halves by a plane parallel to principal axis) then the focal length of each part will remain f.
In this position aperture of prism becomes half, the intensity of the image formed also becomes half (as I ∝ A).
^Combing two convex lenses
^Combing two convex lenses
1. Consider a parallel beam of light incident on a combination of two lenses separated by a distance ‘d’ in air or vacuum.
Case (a):
The final beam after refraction from the two lenses becomes parallel if d = f1 + f2

Case (b):
The final beam after refraction from the two lenses converges at a point situated in between both the lenses if d > f1 + f2 & (d – f1) > f2

Case (c):
The final beam after refraction from the two lenses converges at a point situated outside both the lenses if d < f1

^Combination of lenses
^Combination of lenses
Two or more lenses are combined to
- Increase magnification.
- Make final image erect.
- Reduce certain aberrations.
If two thin lenses of focal lengths f1 and f2 are separated by a distance d then the effective focal length and power of the combination is given by:
1. ![]()
2. P = P1 + P2 – d P1 P2
3. m = m1 x m2 x m3 x – – – – – – – – –
Let us prove the above relations.
* A Zoom lens is based on this result such that f can be varied 0 to ∞ by changing d.



