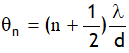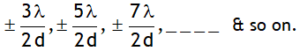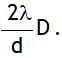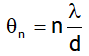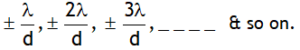^Resolving limit of human eye
^Resolving limit of human eye
For human eye resolving limit is one minute (abbreviated as, 1), this means that the human eye can see two point objects separately if they subtend angle more than one minute of arc at the eye. The diameter of the pupil of human eye is about 2 mm. If we use λ= 5000 A0 to see objects, then the smallest angular separation between two distant point objects that the human eye can resolve is
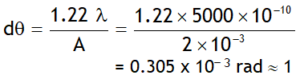
Thus the human eye can see two point objects distinctly if they at the eye an angle equal to one minute of arc. This angle is called the limit of resolution of the eye.
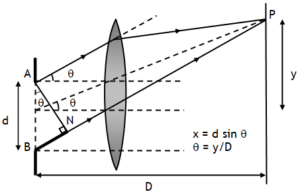
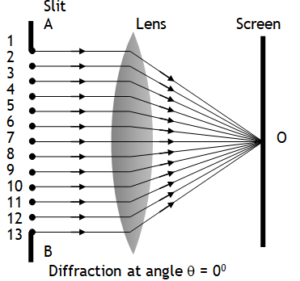
Light rays coming from any object after passing through pupil & eye lens get focused on the retina (screen) in the form of diffraction pattern. We know the maximum intensity of light is diffracted mainly in the central maxima. If the light rays is coming from two objects situated either too close to each other or very far away from eye then their central maxima of their diffraction pattern overlap at the retina, stimulating almost same cells on retina & brain gets one signal & we have perception that we are viewing one object in other words eye fails to resolve (or separate) the two objects if they subtend small angles at eye. e.g. a vehicle with its head lamps ON is approaching us. When the distance of the vehicle from us is large then the angle subtended by the head lamps at the eye is very small, if this is less than one minute then the diffraction pattern of their images at the retina overlap & we have perception of one head lamp. But as the vehicle approaches us the angle subtended by the head lamps at the eye increases, once this angle is more than one minute of arc, diffraction pattern of their images at the retina are formed at different points, exciting retina cells at two different & there by sending two signals to brain & we have perception of two different head lamps now.
Due to the same reason we fail to resolve two nearby stars.

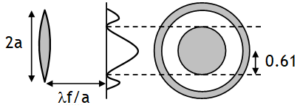
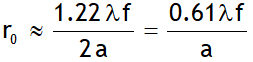
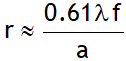 because of diffraction effects. Where f is the focal length of the lens and 2 a (= d) is the diameter of the circular aperture or the diameter of the lens.
because of diffraction effects. Where f is the focal length of the lens and 2 a (= d) is the diameter of the circular aperture or the diameter of the lens.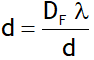
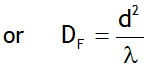
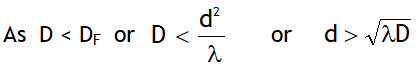
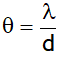
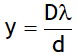
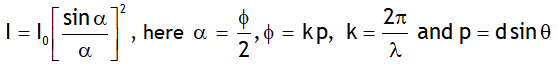
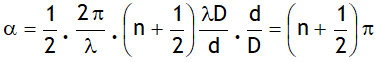
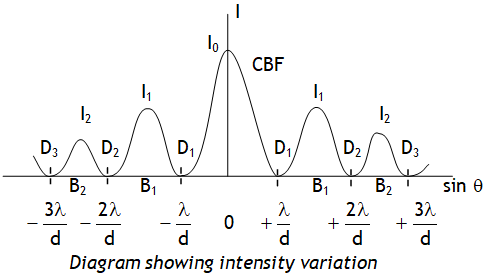
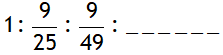
 thus as the slit width is increased, the secondary maxima get narrower. If the slit is sufficiently wide, the secondary maxima disappear and only the central maximum is obtained which is the sharp image of the slit and not a diffraction, thus a distinct diffraction pattern is possible only if the slit is very narrow.
thus as the slit width is increased, the secondary maxima get narrower. If the slit is sufficiently wide, the secondary maxima disappear and only the central maximum is obtained which is the sharp image of the slit and not a diffraction, thus a distinct diffraction pattern is possible only if the slit is very narrow.