^Maxwell equations
^Maxwell equations
Following five equations give a complete description of all em– interactions and are called Maxwell eq:
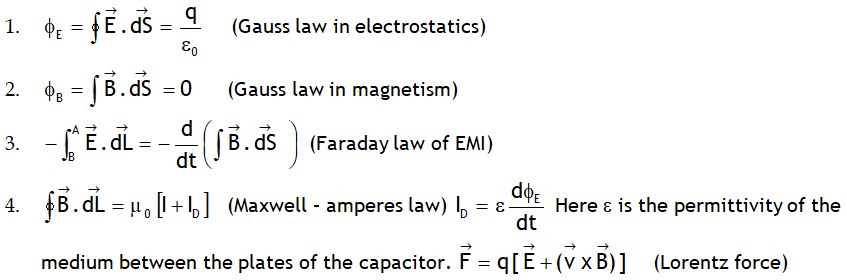
^Maxwell equations
Following five equations give a complete description of all em– interactions and are called Maxwell eq:
^γ – rays
(a) Produced in nuclear reactions and are also emitted by radioactive nuclei (such as Co 60 & Cs 137).
(b) Properties: Effect on photographic plate, fluorescence, ionization, diffraction, high penetrating power & can cause serious damage if absorbed by living tissues.
(c) Used
^Ultraviolet light
(a) Produced by special lamps like mercury and iron are lamps and by very hot bodies like sun.
(b) Properties: Effect on photographic plate, fluorescence, ionization, highly energetic, tanning of the human skin.
(c) Used
^Visible light
^Infra red waves
(a) Also called heat waves & are produced by hot bodies and molecules.
(b) Properties: Heating effect, reflection, refraction, diffraction & propagation through fog.
(c) Used
Cyclotron
Also called magnetic resonance oscillator) & is the first circular accelerator designed was by American Physicist Ernest O. Lawrence. + vely charged particles like proton, deutron & alpha particles etc. can be suitably accelerated by cyclotron. It can’t be used to accelerate light particles (e.g. electrons) & neutral particles (e.g. neutrons).
Charge particle in magnetic field
A point charge moving in uniform magnetic field experiences a force on ![]() . Behaviour of charge particle depends on the angle ‘θ ‘ between
. Behaviour of charge particle depends on the angle ‘θ ‘ between ![]() .
.
Case 1, if θ = 00 or 1800
When the charged particle moves parallel or anti parallel to field then no net force acts on it & its trajectory remains a straight line.
Case 2, If θ is other than 00, 1800 & 900
Charge particle moves in a helical path of radius 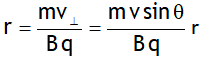 , completes one circle in time
, completes one circle in time 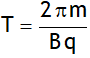 & travels a distance in one time period in the direction of field called pitch & is given by,
& travels a distance in one time period in the direction of field called pitch & is given by,
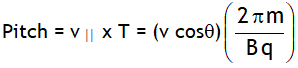
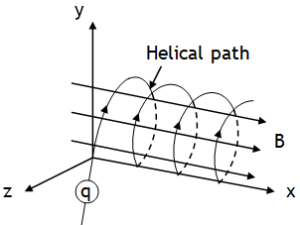
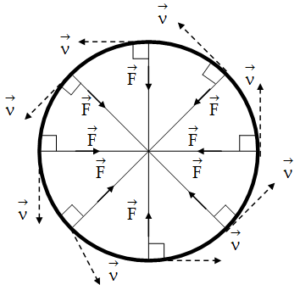
Case 3, If θ is 900
Charge particle moves in a circle at uniform speed.
Radius of circular path is 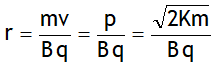
KE of particle is ![]() constant. It completes a cycle in time
constant. It completes a cycle in time ![]() at angular frequency
at angular frequency ![]() .
.
As the force acting on the particle is only normal & no tangential force is available thus speed & hence KE also of the particle will remain unchanged. As the kinetic energy of the charged particle remains constant. Hence no work is done in moving a charge particle moving at right angles to the magnetic field. However due to change in direction ![]() & are variables in direction.
& are variables in direction.
*Average acceleration
Average acceleration is defined as the change in the velocity per unit time spent. If the velocity of a moving body a time t1 when it was at point A is v1. Let at time t2 it reaches point B where is velocity is v2.

Change in its velocity per unit time spent is called average acceleration for an interval.
For motion along x – axis,

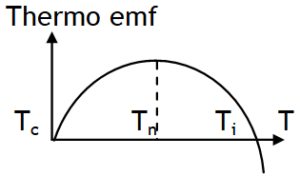
Variation of emf with temp.
The magnitude of & direction depends upon nature of materials of the wires forming thermocouple & difference in temperature of two junctions. For majority of the thermocouples, the temperature dependence of the thermo-emf can be expressed by a quadratic equation,
![]() _ _ _ _ (1)
_ _ _ _ (1)
where α and β are constants for the given pair of metals, called thermoelectric coefficients while θ is the temperature difference between hot and cold junctions.
The above relation holds for a limited range of temperature. Also the variation of thermo emf drawn against temperature difference between hot and cold junctions is found to be parabolic as shown.
Following experimental setup may be used to the effect of temp. on thermo emf for a given thermocouple:
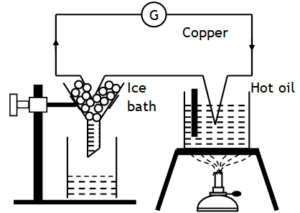
One junction is kept hot by immersing in hot oil bath & the other junction is kept cold by immersing in ice. The temperature of the hot junction can be measured by a thermometer T. The deflection in the sensitive galvanometer G gives a measure of thermo emf.
^Displacement
Suppose a body is moving along a straight line. Let the straight line is along x – axis. Let at a time t1 it was situated at point A at a distance x1 from a fixed point O. Let it moves & at time t2 reaches point B situated at a distance x2 from O.
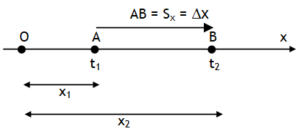
Here the distance AB is called displacement of the body along x axis (Sx) in the time interval t2 – t1 (= Dt). In terms of position coordinates it can be expressed as
Displacement, AB = OB – OA = x2 – x1 or Δx.
i.e. for motion along displacement is equal to the change in position coordinates along that line.