*Rectangular hyperbola
*Rectangular hyperbola
Function xy = c represents a rectangular hyperbola. It meets both x & y axis at infinity only. It is located in quadrant 1 & 3 if c = +ve & in 2 & 4 if c = – ve.
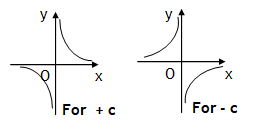
*Rectangular hyperbola
Function xy = c represents a rectangular hyperbola. It meets both x & y axis at infinity only. It is located in quadrant 1 & 3 if c = +ve & in 2 & 4 if c = – ve.

*Straight line
Function y = m x + c represents a straight line cutting + y at acute angle to +x.
m = tanq is called slope of the line.
q = anticlockwise angle made by the line with + x axis.
m = +ve if line makes acute angle to +x.
m = 0 if line is horizontal.
m = – ve if line makes obtuse angle to +x.
c = +ve if line cuts +y.
c = – ve if line cuts -y.
c = 0 if line passes through origin.
*Geometric progression
Example of GP: a, a r, ar2, _ _ _ _ _ _
n th term of an GP: Tn = T1r n – 1
Sum to first n – term of a GP: Sn = 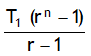
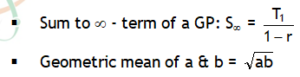
*Binomial expansion
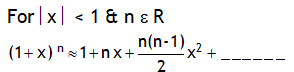
Neglecting the terms containing higher power of x we can write
(1 + x)n ≈ 1 + n x
*Quadratic equation
ax2 + bx + c = 0 (a, b & c ε R with a ≠ 0)
b 2 – 4 a c = D (discriminate)
Roots of quadratic are

The following 6 situations may arise.
If D > 0, then roots are real & unequal.
If D < 0, then roots are imaginary & unequal.
If D = 0, then roots are real & equal.
If D > 0 & a perfect square, then roots are rational.
If D > 0 & not a perfect square, then roots are irrational.
If a = 1, b & c are integers, then roots are rational.
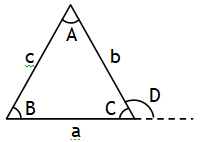
*The three sides and three angles are called its six elements. The angles are represented by the capitals letters A, B and C and the sides are represented by small letters a, b and c. Following results are useful to solve a triangle.

*Range of T – fns
sinθ & cosθ ε [ -1, +1]
tanθ & cotθ ε (– ∞ , +∞)
cosecθ & secθ ε (– ∞, – 1] U [+1, +∞)
^A long horizontal fixed wire carries a current of 100 A. Directly above and parallel to it is another wire carrying a current of 20 A and weighing 0.04 N/m. The separation between the two wires so that the upper wire is just supported by the magnetic repulsion is