^Voltmeter
Voltmeter
(a) Constructed by connecting a high value resistor (H) in series to a galvanometer.
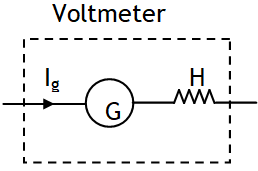
(b) V = I g ( G + H )
(c) RV = G + H → ∝ for ideal
(d) Used in parallel across the resistor whose voltage is to be measured.
Voltmeter
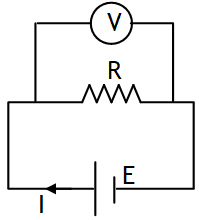
(a) Constructed by connecting a high value resistor (H) in series to a galvanometer.

(b) V = I g ( G + H )
(c) RV = G + H → ∝ for ideal
(d) Used in parallel across the resistor whose voltage is to be measured.

^Least count, accuracy & significant digits
Suppose a rod is measured by a metre stick, and is estimated to lie between 1.6 and 1.8 m, then its length can be written as 1.7 m. It contains two significant digits, of which we are perfectly sure of the position of 1, but slightly doubtful regarding the position of 7.
Now, suppose the same rod is measured by a metre scale graduated to centimetres and is estimated to lie between 173.2 cm & 173.4 cm then its length can be written as 173.3 cm or 1.733 m. Now, the number of significant digits are four namely, 1, 7, 3 and 3 and hence there is an increment in the accuracy of the value. Smaller the least count of a measuring instrument, more will be its accuracy in measurement and accordingly more will be the number of significant digits.
Power transferred theorem
The power transferred by a cell to the load is maximum when R = r & given by
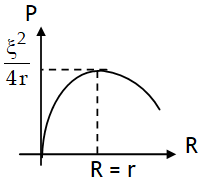
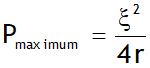
Also then 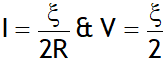
Parallel dielectrics in a capacitor
If three dielectric of slabs of same thickness, but different areas of cross section A1, A2 & A3 , dielectric constants K1, K2 & K3 are placed between the plates of a parallel plate capacitor as shown, then the combination behaves as different dielectrics dividing the plate area are considered as capacitors connected parallel.

Capacitance of this is given by
Cnet = C1 + C2 + C3
![]()
![]()
^What is a Tensor?
A physical quantities which have no specified direction but different values in different directions are called tensors.
Stress, Strain, Density, dielectric constant, refractive index, electrical conductivity, electrical resistivity, moment of inertia etc are tensors. These quantities are taken as tensors at microscopic level & scalars macroscopically.
Following practical units of length are commonly used:
^Uses of dimensions
^Dimensionless Constants
Are the physical quantities which have neither dimensions nor variable values.
e.g. real numbers, e, π etc.
^One radian
One radian (rad) is the angle subtended at the centre of a circle by an arc of length equal to the radius of circle.
*Geometrical Meaning of integration
![]() is called Integral or primitive of y w.r.t. x or anti-differentiation.
is called Integral or primitive of y w.r.t. x or anti-differentiation.
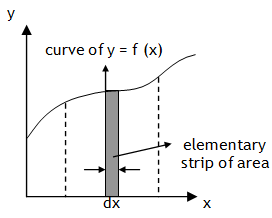
Here, ydx is area of elementary rectangular strip of thickness dx.
Thus 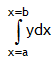 gives the total area bounded by the all the elementary strips of the curve represented by the function
gives the total area bounded by the all the elementary strips of the curve represented by the function
y = f (x) with the x-axis between the limits x = a to x = b. As convention upward areas are taken as positive and downward area negative.
Electrostatic field
If the electric field of a charge at a point doesn’t vary with the time, then the electric field is called electrostatic electric field. It’s effect on other charges is studied by defining two quantities; one a scalar field function called electric field potential ‘V’ & second a vector field function called electric field intensity ![]() are related as
are related as

Here the –ve sign implies that electric field intensity due to both positive & negative charged configuration is always in the direction of decreasing field potential i.e. from a region of high potential to a region of low potential.