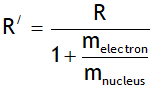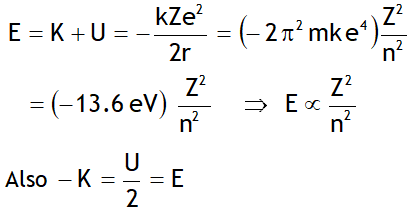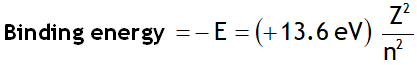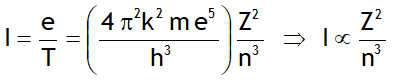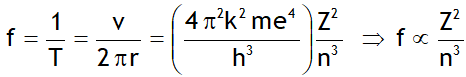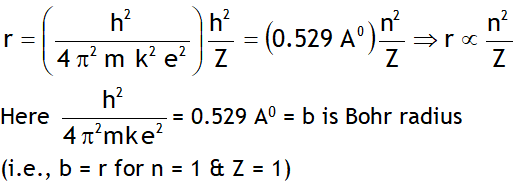^Rydberg’s formula

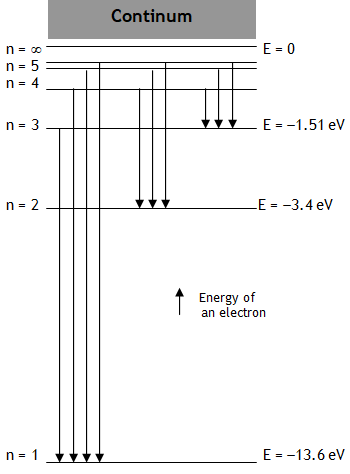
Let ‘E’ be the energy & λ be the wavelength of the photon released when an electron jumps from a higher quantum state of principal quantum number n₂ to a lower quantum state having principal quantum number n₁, then

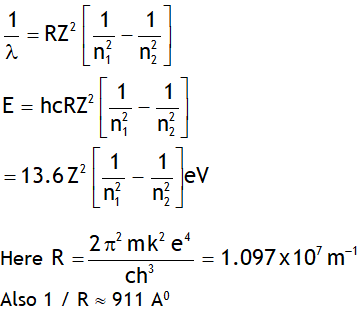
Note Rydberg’s constant depends on mass of

Electron, thus it is not a universal constant.

In deriving the above value the nucleus is assumed to be at rest. However if nucleus is not assumed stationary then the Rydberg constant depends on both mass of electron & nucleus & is given by

^Energy in nth orbit

Here the -ve sign of energy shows that electron is bound to the nucleus & is not free.

The binding energy of the electron in the ground state of the H-atom is called Rydberg. i.e.

1Rydberg = 13.6 eV

^Current generated

^Velocity of electron in nth orbit