^Displacement method

This method is used in the labs to find the focal length of a convex lens.

Consider an object placed between a thin convex lens of focal length ‘f’ & a screen at a distance ‘D’ from the screen.

Using Lens formula for this problem one can write:

To get two distinct images the discriminate > 0.

Thus the essential condition to get two distinct real images on the screen is D > 4 f.

From eqn. (1) the two roots of the quadratic i.e. two different distance of the lens from the object are given by:

From these relations the distance between the two positions of the lens (say ‘x’) can be written as:

The image distance can be written as:

This implies that for the two positions of the lens the image & object distances are interchangeable.

The magnification of the two images can be given by:

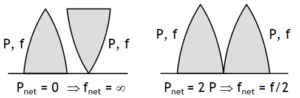
^Combing two convex lenses

1. Consider a parallel beam of light incident on a combination of two lenses separated by a distance ‘d’ in air or vacuum.

Case (a):

The final beam after refraction from the two lenses becomes parallel if d = f₁ + f₂

Case (b):

The final beam after refraction from the two lenses converges at a point situated in between both the lenses  if d > f₁ + f₂ & (d – f₁) > f₂

Case (c):

The final beam after refraction from the two lenses converges at a point situated outside both the lenses if d < f₁

^Image formation by a lens

(a) A concave lens always form virtual, erect & diminished image irrespective of the position of the object.

(b) With a convex lens following possibilities are there

Position of object	Ray diagram	Image produced
At ∞		At F Real (inverted) Extremely Diminished m < < 1
Beyond C i.e. Between ∞ and 2 F		Between F & C Real (inverted) Diminished m < 1
At C		At C Real (inverted) Same as size of object m = 1
Between F and C		Beyond C Real (inverted) Magnified
Object at F		At ∞ Real (inverted) Infinite size m → ∞
Between F and P		Beyond 2 F Virtual (erect) Magnified m > 1

^Curved surface refraction formula

It is a general expression, applicable to both convex & concave surface, for both point & extended object placed in any medium rare or denser, for any type of image formed (real or virtual).

While using this result keep in mind following points:

1. All distance are measured from the pole P (i.e. the centre of surface at which incident ray strikes.
2. μ₁ → Medium from which incident ray comes.
3. μ₂ → Medium towards which incident ray is sent.

^δ without θ

Under this condition

This combination is also called Achromatic prism combination.