^ best physics theory book for neet - KP Physics

*Principle of homogeneity

December 23, 2021/in Back end /by kp-web-admin

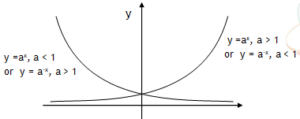
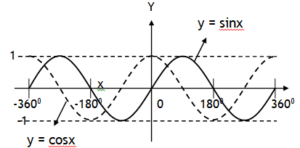
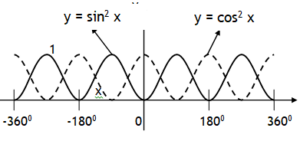
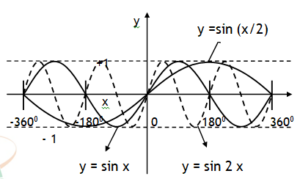
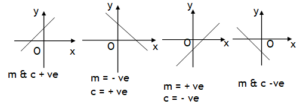
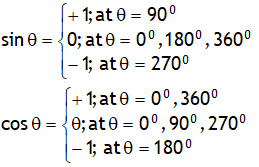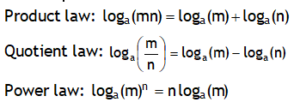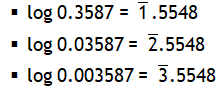*Principle of homogeneity

According to principle of homogeneity of quantities (PHQ) only those quantities can be added or subtracted which have same physical nature.

e.g. Force can’t be added in velocity, similarly or distance can’t be subtracted from time.

Also according to PHQ: L + L = L and L – L = L

L + T = not possible and T – M = not possible.

However there is no restriction on multiplication or division i.e. quantities having same or different dimensions can be both multiplied as well as divided. e.g. v = x/t, F = m.a, P = F/A, W = F.x etc.

^One radian

December 23, 2021/in Back end /by kp-web-admin

^One radian

One radian (rad) is the angle subtended at the centre of a circle by an arc of length equal to the radius of circle.

^Gaussian surface

December 23, 2021/in Back end /by kp-web-admin

Gaussian surface

To find electric field due to a charge configuration using Gauss’s law we draw an imaginary closed surface around that charged distribution.
Gaussian surfaces are normal to electric lines of & symmetric to the charge enclosed such that electric field at every point of the Gaussian surface due to that charged distribution is same.
Gaussian surfaces are spherical for point charges or spherical distribution of charges & cylindrical for linear and planar distribution of charge.
Only those charges which lie inside the Gaussian surface are considered & that located outside have no contribution in the flux.
Discrete charges on the surface of the -Gaussian surface are not considered (as electric field at the location of a discrete charge is not defined) but continuous charges can be considered.

^For infinite line charge

December 23, 2021/in Back end /by kp-web-admin

For infinite line charge

Both α & β will approach to 90⁰ & E becomes

*Integral calculus

December 23, 2021/in Back end /by kp-web-admin

*Integral calculus

Integration is the reverse process of differentiation, thus also called anti-differentiation.

Suppose we have a function g (x) whose derivative.

The function g (x) is known as the indefinite Integral of f (x) and is denoted as:

1/d is usually abbreviated by the symbol ∫ (called integral), so one can write

∫ f (x) dx = g (x) + c

Here c is called constant of integration. Its value is arbitrary and can be calculated form the information given in the problem.

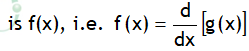
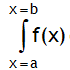Integral of the form is called definite integral. Here x = a & x = b are called limits of integration. x = a is called lower limit & x = b is called upper limit. If limits are not given, then the integration is called indefinite integration.

Definite integral is a number. Indefinite integral has no limits; it is a function. No integration constant is required in the final answer in definite integrals. Following examples explain how one can derive integration from differentiation.

^Charge is source of field

December 23, 2021/in Back end /by kp-web-admin

Charge is source of field

An electric charge at rest produces only electric field around it.
An electric charge moving with uniform velocity produces both electric and magnetic fields around it but radiates no energy.
An accelerated charge produces both electric and magnetic fields around it as well as radiates energy in the form of electromagnetic waves.