^Bohr’s frequency condition
^Bohr’s frequency condition
Energy is emitted only when an electron exited to the higher states jumps back to lower states. The energy emitted is described by the relation
h f = E1 – E2
Ionization energy = +13.6 eV Z2
Posts
^Energy level diagram
^Energy level diagram
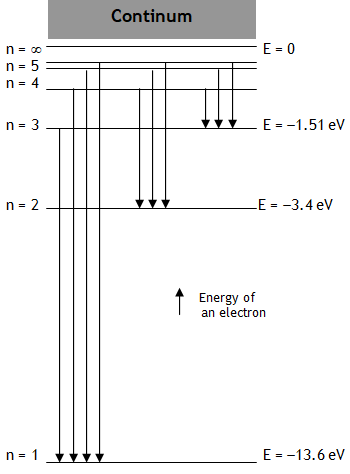
With the increase in the value of principle quantum number n
(a) r, L, T, U & E all increase while
(b) v, K, & w all decrease.
^Accelerated body
^Accelerated body
If with the passage of time the state of a body changes i.e. its velocity w.r.t. ground decreases or increases or changes in direction then the body is said to be accelerated. Some external force is required to change the state of the body.
^Energy in nth orbit
^Energy in nth orbit
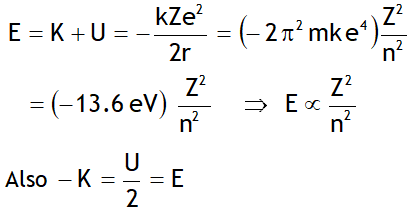
Here the -ve sign of energy shows that electron is bound to the nucleus & is not free.
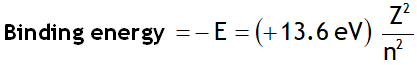
The binding energy of the electron in the ground state of the H-atom is called Rydberg. i.e.
1Rydberg = 13.6 eV
^Magnetic moment generated
^Magnetic moment generated
^Current generated
^Current generated
^Frequency of revolution
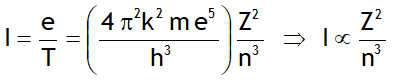
^Frequency of revolution
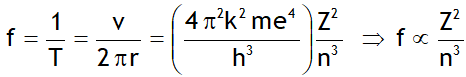
For n = 1, Z = 1; f = 6.57 x 1015 revolutions/s
^Velocity of electron in nth orbit
^Velocity of electron in nth orbit
^Radius of nth orbit
^Radius of nth orbit
^Angular momentum quantization
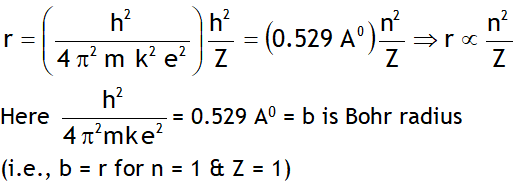
^Angular momentum quantization
An electron can revolve around the nucleus only in those orbits where the circumference of the orbit is integral multiple of the wavelength. Such orbits are called stationary.
Here 
is the minimum value of angular momentum in the first orbit of any H-like atom.
Frank-Hertz experiment (1914) experiment experimentally demonstrated the existence of discrete stationary orbits.
