*The Seven Fundamental Quantities
*The Seven Fundamental Quantities
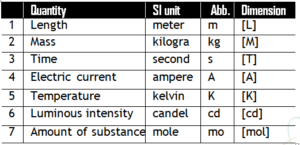
*The Seven Fundamental Quantities

Gaussian surface
For infinite line charge
Both α & β will approach to 900 & E becomes

*Integral calculus
Integration is the reverse process of differentiation, thus also called anti-differentiation.
Suppose we have a function g (x) whose derivative.
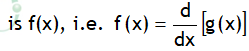
The function g (x) is known as the indefinite Integral of f (x) and is denoted as:
1/d is usually abbreviated by the symbol ∫ (called integral), so one can write
∫ f (x) dx = g (x) + c
Here c is called constant of integration. Its value is arbitrary and can be calculated form the information given in the problem.
Integral of the form 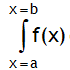 is called definite integral. Here x = a & x = b are called limits of integration. x = a is called lower limit & x = b is called upper limit. If limits are not given, then the integration is called indefinite integration.
is called definite integral. Here x = a & x = b are called limits of integration. x = a is called lower limit & x = b is called upper limit. If limits are not given, then the integration is called indefinite integration.
Definite integral is a number. Indefinite integral has no limits; it is a function. No integration constant is required in the final answer in definite integrals. Following examples explain how one can derive integration from differentiation.

Charge is source of field
*Graph of exponential functions
Functions y = ax, a < 1 & y = a– x, a > 1 are exponentially decreasing. Functions y = ax, a > 1 & y = a– x, a<1 are exponentially increasing.
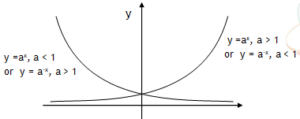
The y intercept of the function y = ax is point (0, 1). If a = e (2.71828) then y = ex is called natural exponential function.
*Up or down parabola
A quadratic of the form y = ax2 + bx + c represents an upward or a downward parabola, it can also be expressed by the following function
(x – u)2 = L (y – v)
L= +ve for upward parabola & L = – ve for a downward parabola.

*Trigonometric functions
We know following values for sinθ & cosθ.
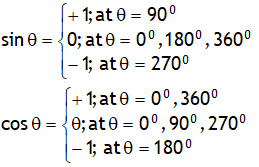
Using these values we can plot the following graphs:
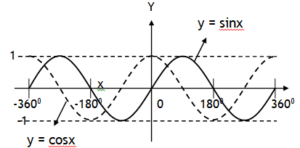
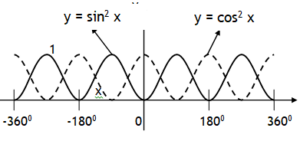
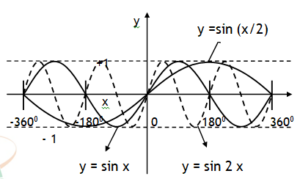
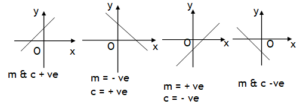
Note the function y = sinx completes one cycle at 3600 where as y = sin2x completes it at 1800 & at
y = sinx/2 completes it at 7200.
*Laws of log
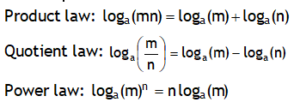

Examples
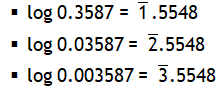
*Componendo & dividendo
