^Ammeter
Ammeter
(a) Constructed by connecting small resistance called shunt (S) in parallel to a galvanometer.
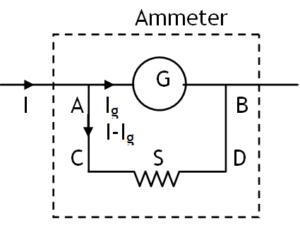
(b) Ig G = (I – Ig) S
(c) 
(d) Used in series with the resistor whose current is to be measured.
Posts
^Power transferred theorem
Power transferred theorem
The power transferred by a cell to the load is maximum when R = r & given by
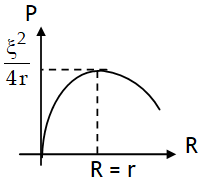
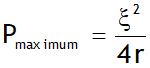
Also then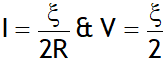 
^Significant figures
^Significant figures
All accurately known digits plus the first uncertain digit of a measurement is called significant digits or significant figures. e.g. if in a measurement, mass of a body lies between 5.6 kg & 5.7 kg & we estimate it as 5.62 kg then the first two digits 5 & 6 are certain while the third digit 2 is approximately known we can say there are 3 significant figures.
Following are the rules for counting significant figures
Rule 1: All non zero digits are significant.
Rule 2: All zeros occuring between two non zero digits are significant.
Rule 3: The digit zero (underlined) conventionally put on the left of a decimal for a number less than one is never significant. All zeros to the right the decimal point are not significant.
Rule 4: The terminal or trailing zero(s) in a number without a decimal point are not significant.
Rule 5: The trailing zero(s) in a number with a decimal point are significant.
Rule 6: The powers of ten are not significant.
Rule 7: No. of significant figures remains unchanged on changing the units of measurement, zeroes appearing in the base number in the scientific notation are significant.
| Example | NSD | Using rule |
| 4567 | Four | 1 |
| 450067 | Six | 2 |
| 0.004567 | Four | 3 |
| 456700 | Four | 4 |
| 0.00456700 | Six | 5 |
| 4.5 x 10 – 6 | Two | 6 |
| 5.300 x 10 6 mm | Four | 7 |
^Series combination of resistors
Series combination of resistors
The current across each circuit element is same, but potential difference is different & proportional to resistance of that part.
i.e. I = I1 = I2 = I3 & V1 = IR1, V2 = IR2, V3 = IR3 & R series = R1 + R2 + R3
^Electric resistance
Electric resistance
Depends upon the nature of material, shape & size, physical state like temperature, pressure, type & extent of impurity etc. of conductor. However r depends upon all above factors except on shape & size.
^Series dielectrics in a capacitor
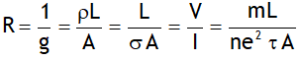
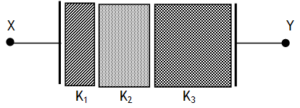
Series dielectrics in a capacitor
If three dielectric slabs of thickness t1, t2 & t3, dielectric constants K1, K2 & K3 are placed between the plates of a parallel plate capacitor as shown, then the combination behaves as different dielectrics dividing the spacing are considered as capacitors connected in series.
Capacitance of this is given by
^Energy (potential) stored in a capacitor
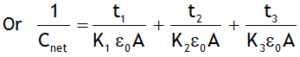
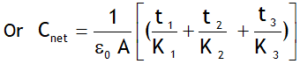
Energy (potential) stored in a capacitor
A charged capacitor of any shape or size stores energy (potential) in the form of electrostatic electric field, it is given by
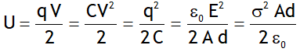
Energy per unit volume is called energy density, it is Electric energy density,
^What is a vector?
^What is a vector?
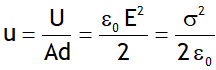
If both magnitude and direction are required to completely described a physical quantity, then it is called a vector. A vector quantity is represented by putting on arrow above it or by bold letter e.g. it Q is vector then we represent it as or Q. if a quantity can have any direction it is called polar. If its direction is along axis only then called axial.
^Dimensionless Quantities
^Dimensionless Quantities
Strain, angle, solid angle, all Trigonometric ratios, all real numbers, logarithmic functions, exponential functions, Poisson’s ratio, refractive index, relative density, relative permittivity, relative permeability, fine structure constant etc. have no dimensions.
^Field due to sheets
Field due to sheets
Using Gauss law we can prove that electric field sheets of charge density σ
1. 
near a infinite sheet or thick sheet
2. 
near a finite sheet or thin sheet
