^Atomic mass unit (u)
^Atomic mass unit (u)
Posts
^Bohr correspondence principle
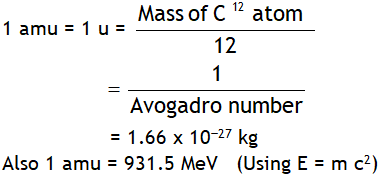
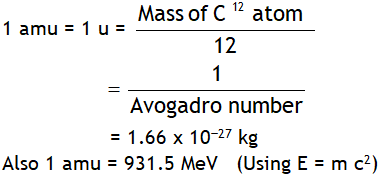
^Bohr correspondence principle
According to this principle the quantum theory must give same result as classical theory in the appropriate classical limit.
^Limitations of Bohr’s theory
^Limitations of Bohr’s theory
- It is valid only for single electron system.
- Nucleus was taken as stationary but it also rotates about its own axis.
- Couldn’t explain fine structure of spectral line.
- Provides no information about the relative intensities of spectral lines.
- Provides no distribution of electrons in an atom.
- Fails to explain that why do the electrons move only in circular orbits.
- Bohr’s theory doesn’t explain the Zeeman effect (splitting up of spectral lines in magnetic field) & Stark effect (splitting up of spectral lines in electric field).
- Bohr’s theory doesn’t explain the doublets in the spectrum of the some atoms e.g. in sodium (5890 A0 & 5896 A0).
- Silent about the selection rules which governs the transitions.
- Use two theories
(i) Quantum (to explain the existence of stationary orbits) &
(ii) Classical (for motion of electrons in the orbits). These two theories essentially oppose each other.
^Spectrum of hydrogen atom
^Spectrum of hydrogen atom
^Rydberg’s formula
^Rydberg’s formula
Let ‘E’ be the energy & λ be the wavelength of the photon released when an electron jumps from a higher quantum state of principal quantum number n2 to a lower quantum state having principal quantum number n1, then
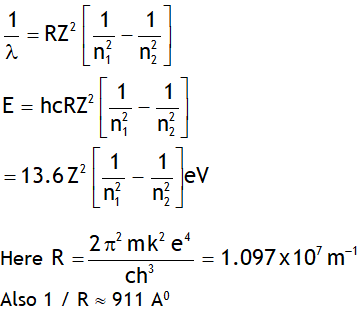
Note Rydberg’s constant depends on mass of
Electron, thus it is not a universal constant.
In deriving the above value the nucleus is assumed to be at rest. However if nucleus is not assumed stationary then the Rydberg constant depends on both mass of electron & nucleus & is given by
^Bohr’s frequency condition
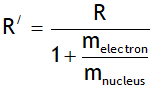
^Bohr’s frequency condition
Energy is emitted only when an electron exited to the higher states jumps back to lower states. The energy emitted is described by the relation
h f = E1 – E2
Ionization energy = +13.6 eV Z2
^Energy level diagram
^Energy level diagram
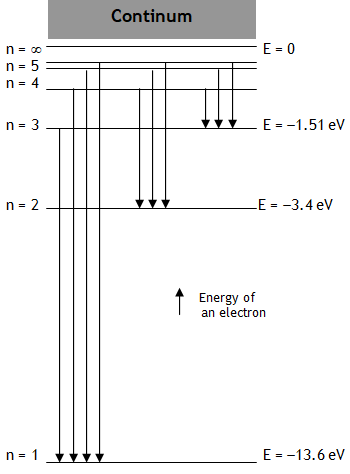
With the increase in the value of principle quantum number n
(a) r, L, T, U & E all increase while
(b) v, K, & w all decrease.
^Examples of inertia
^Examples of inertia
- More initial effort is required to set up heavy objects in motion. Also more effort is required to stop them or change their direction.
- A man stepping out of a moving bus falls with his head in the forward direction. As otherwise due to inertia of motion the upper part of his body will be in motion & feet on touching the ground will come to rest. Due to this, unbalanced forces acting on his body may cause him to fall down.
- A clean hole is made when a bullet is fired at a glass window pane, while it is broken into pieces by a stone. Due to small speed, the stone remains in contact with the windowpane for a longer duration, thus transferring its motion to the pane & beaks it into pieces. On the other hand the particles of windowpane near the hole are unable to share the rapid motion of the bullet & remain undisturbed.
- Place a coin on a playing card covering a glass. On giving a sudden jerk to the card, the card flies off and the coin drops into the glass. This is because the coin tends to remain at rest due to inertia of rest.
- Consider the shown situation. A mass M suspended from a rigid support by means of string A is pulled down by applying a force F on another thread B. When a jerk is given to string B, the upper portion of the system is not able to share the force in short time and the block tends to remain at rest due to inertia of rest & consequently the string B breaks. While if we apply a steady force to string B, the force gets sufficient time to reach the position A & consequently the string A breaks.
- When a dog chases a hare, the hare runs along a zig-zag path. The dog
has more mass and hence has more inertia of direction than that of hare, thus it becomes difficult for the dog to catch the hare.
- Suppose a stone is whirled in a circle at the end of a string. The velocity of the stone at any instant is along the tangent to the circle. When the string suddenly breaks, the stone flies off tangentially due to directional inertia. As earlier their direction of motion at any point was along the tangent to that point & due to inertia of direction the stone has a tendency to maintain its direction of motion.
^Energy in nth orbit
^Energy in nth orbit
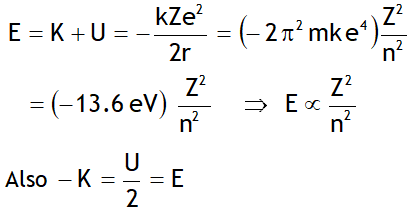
Here the -ve sign of energy shows that electron is bound to the nucleus & is not free.
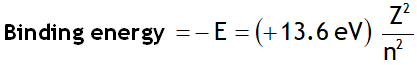
The binding energy of the electron in the ground state of the H-atom is called Rydberg. i.e.
1Rydberg = 13.6 eV
^Magnetic moment generated
^Magnetic moment generated
