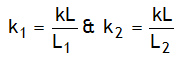^Spring force, Fsp

^Spring force, F_sp

A spring because of its elasticity has a tendency to resist its deformation (compression or stretching, x). It does so by producing a force that restores it back to its relaxed position, this force is called the spring force & varies linearly with the deformation given to spring.

F_sp = – kx for x << L.

 

Here k is called stiffness constant or force constant or elastic factor of the spring. It depends inversely on the length of the spring & directly on the elasticity (Young’s modulus, Y) of material used in making the spring.

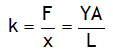
A is area of cross sectional of the material.

Using this property we can say that.

a. If a spring is cut into n equal parts then force constant of each part will be nk.

b. If a spring of length ‘L’ is cut into two parts whose lengths are in ratio L₁ : L₂, then the force constants will be: