*Sin & cos as projections

*Sin & cos as projections

Actually cos & sin gives us an ideas of projections (shadows) of a line on x & y axis respectively. Consider a line of length L making an anticlockwise angle q with + x axis. Let L_x (= ON) &L_y (= OM) be its x & y projections, then

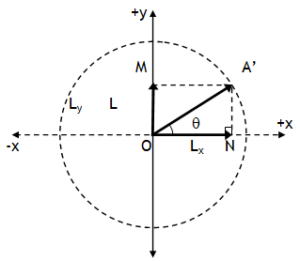
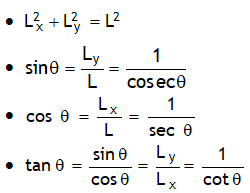
If θ is increased from 0⁰ to 90⁰, then cosθ decreases & sinθ increases.

sin² θ + cos² θ = 1

cosec² θ – cot^{2 θ} = 1

For integral values of n