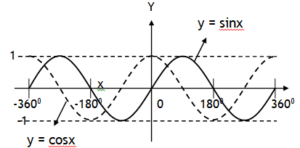
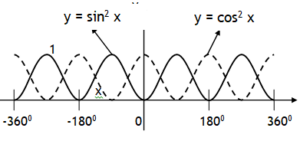
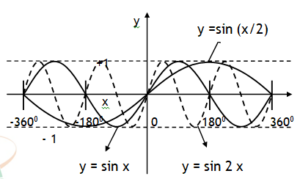
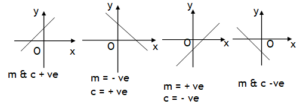
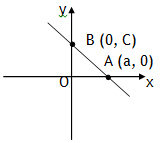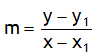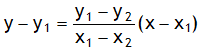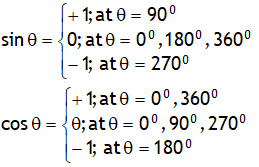*Right handed or left handed parabola
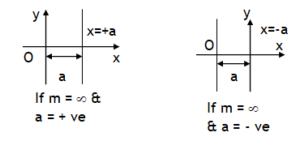
A quadratic of the form x = ay2 + by + c represents an right handed or a left handed parabola, it can also be expressed by the following function
(y – v)2 = L (x – u)
Here (u, v) represent coordinates of vertex (V) of a parabola. L= +ve for right handed parabola &
L = – ve for a left handed parabola.
*Up or down parabola
A quadratic of the form y = ax2 + bx + c represents an upward or a downward parabola, it can also be expressed by the following function
(x – u)2 = L (y – v)
L= +ve for upward parabola & L = – ve for a downward parabola.
*Parabola
Parabola is an open figure & can be defined as the locus of a point P which moves in a plane so that its distance from a fixed point (called Focus, F) bears a constant ratio (called eccentricity, e = 1) to its distance from a fixed straight line (called directrix).
*Intercept form
Suppose a line cuts x axis at point A (a, 0) and cuts y axis at a point B (0, C), then it can be described by the equation,
[called intercept form].
*Point slope form
Equation of a straight line having slope m and passing through a point A (x1, y1) is 
2 point form
Equation of a straight line passing through two point A (x1, y1) and B (x2, y2) is 
*Vertical line
Function x = a represents a vertical line located right side of y axis if a = +ve & left side of y axis if a = – ve.
*Straight line
Function y = m x + c represents a straight line cutting + y at acute angle to +x.
m = tanq is called slope of the line.
q = anticlockwise angle made by the line with + x axis.
m = +ve if line makes acute angle to +x.
m = 0 if line is horizontal.
m = – ve if line makes obtuse angle to +x.
c = +ve if line cuts +y.
c = – ve if line cuts -y.
c = 0 if line passes through origin.
*Trigonometric functions
We know following values for sinθ & cosθ.
Using these values we can plot the following graphs:
Note the function y = sinx completes one cycle at 3600 where as y = sin2x completes it at 1800 & at
y = sinx/2 completes it at 7200.
*Shape of y versus x graph
Let a physical quantity y depends on other physical quantity x, this dependence is called a mathematical function & usually expressed as
y = f (x) (read as y is a function of x).
The dependence of y on x can be visualised by drawing a graph of function y = f (x). While plotting graphs the independent varaible is taken on horizontal line & dependent on vertical line. Shape of y versus x graph depends on the type of function.
Following types of y versus x graphs are frequently encountered in Physics.
*Mean of n terms
If x1, x2, _ _ _ _ _ _ _ _ _ , xn be n quantities then their
If A, G and H be A.M., G.M. and H.M. between two numbers, then
(a) A ³ G ³ H,(b) G2 = A .H
Series
Call 9872662552