Charge is source of field
Dielectric constant
Dielectric constant is also called relative permittivity or specific inductive capacity & is defined as
K = 1 (air or vacuum), K = 81 (water),
K = ∞ (metals), K = 0 (insulator)
Dielectric constant decreases on heating.
Coulomb’s Law
Force of interaction (attraction or repulsion) between two static point charges is called electrostatic forces. For two static point charges electrostatic forces is described by Coulomb’s law
is called electrostatic constant. The quantity eo is called permitivity of free space (vacuum /air). Its value is eo = 8.98755 x 10 –12 N– 1 m – 2 C 2
Dimensions of permittivity: [M – 1 A2 L– 3 T4 ]
Charge which exerts force is called source & which experiences it is called victim.
*Properties of charge
1. Charge is scalar, i.e. has no direction.
2. Charge is additive i.e. total charge on a body is given by addition of individual charges for discrete distribution & by integration for continuous distribution.
3. Charge is conserved in any isolated process
4. Charge is quantized i.e. charge smaller than electronic charge, e = 1.6 x 10 – 19 C (also called elementary charge.) is not possible and exists in integral multiple of e i.e. mathematically.
Q = Ne, here N is an integer.
5. Charge is invariant of space, time & velocity.
6. Charge is can’t exist without mass.
*Graph of exponential functions
Functions y = ax, a < 1 & y = a– x, a > 1 are exponentially decreasing. Functions y = ax, a > 1 & y = a– x, a<1 are exponentially increasing.
The y intercept of the function y = ax is point (0, 1). If a = e (2.71828) then y = ex is called natural exponential function.
*Graph of logarithmic function
The function y = logb x is called a logarithmic function, it is not defined for x ≤ 0.
It is a decreasing function for 0 < b & increasing for b > 1. The y – axis is an asymptote of the curve
y = logb x. The x intercept is the point (1, 0).
*Ellipse
An ellipse is a closed curve like a circle. An ellipse may be drawn by choosing two points F1 and F2, each of which is a called a focus, and then drawing a curve through points for which the sum of the distances PF1 and PF2, respectively, is a constant.
If the center of ellipse is at point origin
Note if a = b, ellipse becomes a circle of radius a.
Area of ellipse = πab
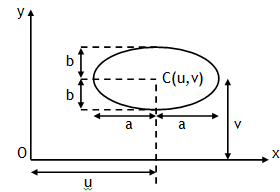
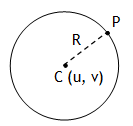
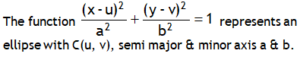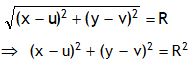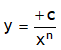*Circle The locus of a point P (x, y) which moves in a plane so that its distance from a fixed point is always a constant. The fixed point is called the centre C (u, v) of the circle and the constant distance is called its radius (R).
Also a radius of a circle is a straight line joining the centre any point on the circumference. As CP = R, thus using displacement formula we can write
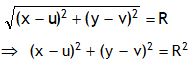
The above expression is called Central form of a circle.
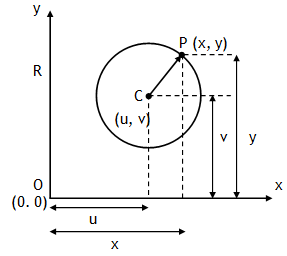
A circle can also be expressed as
ax2 + by2 + 2 gx + 2 fy + c = 0
This expression is called general form of a circle.
Here (-g, -f) is the center of the circle
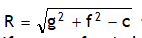is radius
If centre of a circle coincides with origin O (0, 0) then the above expression can be written as,
x2 + y2 = R2.
This expression is called Standard form of a circle.
*Inverse function
Function of the form, 
have the shown variation. All the curves pass through the point (1, 1). For n > 1 the graph lies above the rectangular hyperbola
(n =1) in the region
0 < x < 1 and then lies below it in the region x > 1. For 0 < n < 1 the graph first lies below the hyperbola in the region 0 < x < 1 and then lies above the hyperbola in the region x > 1.
*Rectangular hyperbola
Function xy = c represents a rectangular hyperbola. It meets both x & y axis at infinity only. It is located in quadrant 1 & 3 if c = +ve & in 2 & 4 if c = – ve.
Call 9872662552