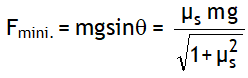^Oblique pull
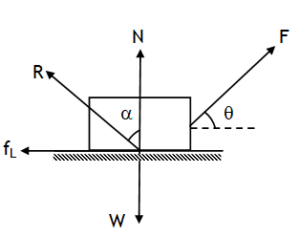
Suppose a block of mass ‘m’ placed on a rough horizontal plane is pulled by a constant force F acting at an angle θ to horizontal,
let Fsinθ < mg, then, N = mg – Fsinθ
Force needed to start the block moving is,
Fcosθ = fL
Using law of friction the limiting friction is,
fL = μS N
Combining above equations, we get,
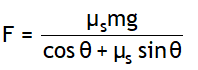
Using tanα = μS, we get, 
At θ = α, the force required to pull becomes minimum & given by
^f versus F graph
For the static body the f versus F graph will be a straight line passing through origin making an angle 450 with the F axis. It will be a horizontal line when the body starts moving, because kinetic friction is constant.
^Motion of a body on a fixed rough horizontal surface
Suppose a block of mass ‘m’ placed on a rough horizontal plane is pulled by a horizontal force F.
Following are the various possibilities:
^Oblique pulling is easier than pushing
Let 1 → oblique pushing & 2 → oblique pulling
⇒ Force required for oblique pushing is greater than that for oblique pulling. i.e. oblique pulling is easier than oblique pushing. Check yourself that there is no difference between pushing & pulling if the force applied is horizontal.
^Angle of friction
The angle between the normal reaction & the resultant of normal reaction & limiting friction on a horizontal rough surface is called angle of friction (α).
On an inclined plane angle of friction is also called angle of repose (β).
α = β = tan– 1(μstatic)
^Condition to start relative motion
Suppose a body A at rest over another body B. Let the limiting friction acing between them is fLAB. If a net force F acts on A which tends to start motion of A relative to B then the condition to start motion of A relative to B is F > fLAB. If F > fLAB then A will remain at rest relative to B. However if
F > fLAB then A accelerates relative to B & a kinetic friction between A & B acts.
^Static friction, fk
The frictional force acting between two surfaces at rest with respect to each other is called static friction. Static friction is a self adjusting force. It adjusts itself from zero to a maximum value called limiting friction.
fs = 0 to μs N (called fL)
^Coefficient of friction
^Kinetic friction, fk
Frictional force acting between two surfaces moving with respect to each other is called kinetic friction. Kinetic friction is independent of amount of velocity. Its amount is given by fk = mk N.
Here μk is called coefficient of friction.
^Friction, f
A tangential contact force opposing relative motion between two surfaces is called friction.
It is two types static & kinetic.
Call 9872662552