^Non-conservative force
^Non-conservative force
Friction, viscous drag. Mechanical energy is dissipated.
^Conservative forces
^Conservative forces
Gravitational, electromagnetic & spring. Mechanical energy (= K + U) is conserved.
^Pendulum in accelerated frame
^Pendulum in accelerated frame
Suppose a simple pendulum is hanging in a truck speeding up horizontally tight side with acceleration ‘a’ w.r.t. stationary ground, then
From the ground frame
- Tsinθ gives the pendulum x acceleration (a)
i.e. Tsinθ = ma
- Tcosθ balances the weight of the pendulum
i.e. Tcosθ = mg
From the truck frame
- the pendulum is in eqbm. Under the influence of three forces pseudo force, weight & tension in string, i.e.,
- Tsinθ balances the x force on pendulum i.e. Tsinθ = ma
- Tcosθ balances the weight of the pendulum i.e. Tcosθ = mg Note from both the final rearrangement of equations gives same relations. Also from the drawings or equations we can write
^Weight in a lift
^Weight in a lift
Consider a person 1 of mass m (true weight, mg) standing on a weighing scale placed on the floor of a lift. The reading (R) of weighing scale is called his apparent weight, the scale by the person.
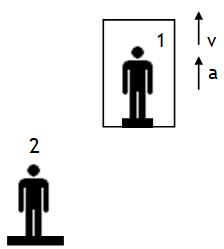
Let the lift is speeding up with acceleration ‘a’ w.r.t. a stationary ground observer 2 (inertial). Using NSL from the frame of reference of 2 we get:
N – mg = ma _ _ _ _ (1)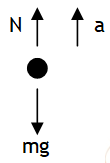 
Person 1 is in a non inertial frame, thus experiences a pseudo force (ma) opposite to acceleration of lift frame & is stationary w.r.t. lift under the influence of mg, N & ma, thus
(-mg) + (+N) + (-ma) =0 _ _ _ _ (2)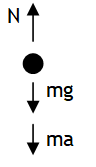 
From (1) & (2) we are getting same result
N = R = m (g + a).
1. R = m (g + a), if the lift moves
(a) upward with uniform acceleration or
(b) downward with uniform deceleration.
2. R = m (g – a), if the lift moves
(a) upward with uniform deceleration or
(b) downward with uniform acceleration.
3. R = m g, if the lift moves
(a) upwards with constant velocity or
(b) downwards with constant velocity or
(c) if the lift is at rest.
4. R = 0, if the lift falls freely under gravity i.e. (a = g).
^A horizontal rod pulled
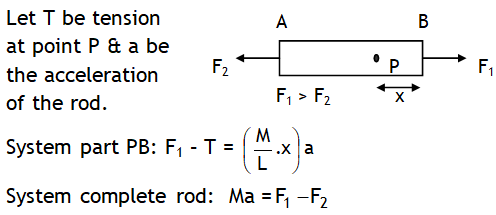
^A horizontal rod pulled
^A block hanging on two strings
^A block hanging on two strings
^A block hanging on two strings
^A block hanging on two strings
^Tension, T
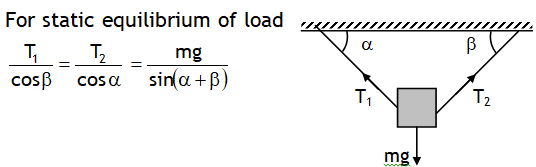
^Tension, T
Restoring force developed in wires, sheets & rods is called tension force. It is equals to reaction of net pull.
^Lemi’s theorem
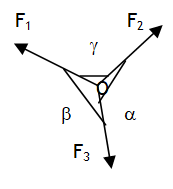
^Lemi’s theorem
It is used to solve situations based on Equilibrium of three concurrent coplanar forces. Let F1, F2 & F3 the three concurrent coplanar forces in equilibrium at point O as shown in the diagram. Then using Lemi’s theorem we can write: 
^Static equilibrium
^Static equilibrium
A body at rest is called static equilibrium.
However momentary rest is not equilibrium. e.g. a projectile at its highest point or an oscillating body at its extreme position are at rest (momentary) thus not in equilibrium.
