^Maximum deviation
^Maximum deviation
A prism shows maximum deviation when incidence angle is maximum i.e. 900, also then
- δmax. = 900 + e – A
- r1 = C
- e = sin–1 [μ sin (A – C)]
Posts
^Minimum deviation
^Minimum deviation
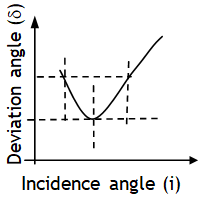
If a light ray is incident at an angle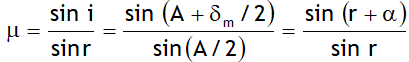 
then it shows minimum deviation, also then
1. 
2. Refracted ray travels parallel to base of the prism if the prism is equilateral
3. δmin. = 2 i – A = 2 i – 2 r = 2 α
4. 
An equilateral prism (i.e. prism angle A = 600) made of ordinary glass (i.e. μ = 1.5) & placed in air (i.e. μ1 = 1), at incidence angle of the 490 shows minimum deviation of 380 with refraction angle of 300.
^Deviation of the emergent ray
^Deviation of the emergent ray
Incident ray deviates clockwise towards the base at first face by amount δ1 (= i1 – r1) & then again deviates clockwise towards the base at second face by amount δ2 (= r2 – i2), thus the total deviation of the prism sum of δ1 & δ2 . Also from the cyclic quadilaternal AEHF,
r1 + i2 = A. From this information we can write
δ = δ1 + δ2 = i1 + r2 – A [Called Prism equation
For given μ, λ & A with the increase of incidence angle deviation angle first decreases & becomes minimum & then starts increasing as shown in the graph.
^Prism
^Prism
Prism angle A is also called refracting angle & not angle of refraction.
A light ray DE in incident on the first face AB of a prism ABC at an incidence angle i1. The refracted ray EF bends towards the base BC of the prism has a refraction angle r1 & strikes the second face AC of the prism at an incident angle i2. If i2 < C, then the light ray striking the face AC undergoes refraction & emerges out from the prism as the emergent ray FG.
^Normal shift
^Normal shift
Consider on object O in medium 1 (μ1 > μ2) & observer with eye E in medium 2.
^Critical angle
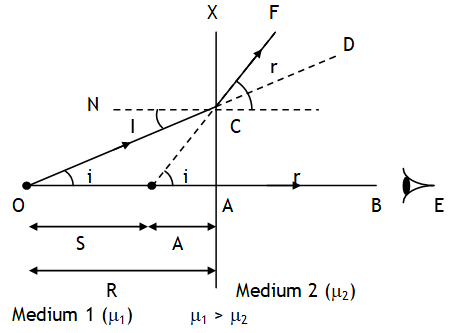
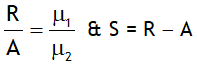
^Critical angle
It is that angle of incidence (i = C) at which a ray going from denser to rare medium shows grazing emergence (r = 900).
^Optical path (L)
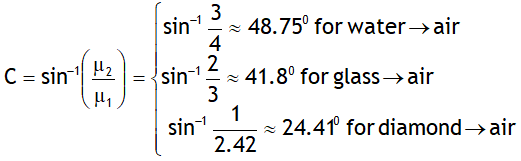
^Optical path (L)
Distance travelled by light in vacuum in the same time in which it travels a given path length in a medium. If light travels a path length d in a medium at speed v, the time taken by it will be d/v.
Thus optical path length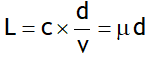 
As μ > 1, optical path length is always greater than geometrical path length.
^Refraction
^Refraction
1. Snell’s law is the law of refraction. It is applicable for both plane & curved surfaces. According to this law the product μ sinθ remains constant in any medium. Thus for a light going from medium 1 to 2
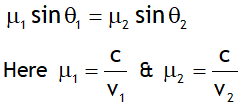
When a light wave enters a denser medium (say glass) from a rarer medium (say air)
2. The frequency (f) of the wave & hence the colour of the light wave remains the same
3. But the wavelength of the wave decreases μ times as a result its speed of the light wave decreases μ times (because v = f λ)
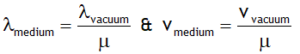
4. However in refraction of light, the amplitude of light may decrease or remain constant.
5. There is no change of its phase i.e. ΔΦ = 0.
6. No. of waves in ‘t’ thickness of a medium are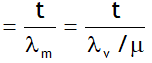 
^Optical refractive index
^Optical refractive index
^Uses of Convex mirror
^Uses of Convex mirror
- As back view mirror in vehicles due to its greater field of view & it always virtual, erect & diminished image for a real object irrespective of the position of the object.
- For reflectors in street lamps.
- Anti – shoplifting mirrors
- In refracting type telescopes.
- For decoration purposes (as they form small beautiful images).
