^At centre of arc
At centre of arc
Magnetic field at centre of arc is ![]()
Use θ in radians.
Contribution of straight parts at C is zero.
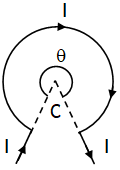
At centre of arc
Magnetic field at centre of arc is ![]()
Use θ in radians.
Contribution of straight parts at C is zero.

^Instantaneous acceleration
Acceleration at a particular instant of time is called instantaneous acceleration. Mathematically it is measured as the limiting value of the average acceleration.
For motion along x – axis,=
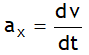
For 1 D motion along x – axis we have,
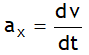
i.e. instantaneous acceleration is equal to slope of velocity time graph (v – t).
On separating the variables & integrating this relation can be rearranged as
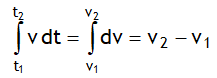
i.e. area under v – t graph bounded with the time axis for a time interval is equal to change in velocity for that time interval.
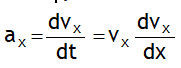
i.e. instantaneous acceleration is slope of velocity time graph (v – t) or velocity times slope of v – x graph.
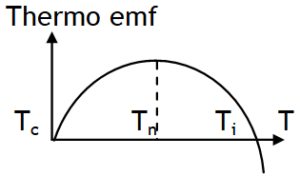
Variation of emf with temp.
The magnitude of & direction depends upon nature of materials of the wires forming thermocouple & difference in temperature of two junctions. For majority of the thermocouples, the temperature dependence of the thermo-emf can be expressed by a quadratic equation,
![]() _ _ _ _ (1)
_ _ _ _ (1)
where α and β are constants for the given pair of metals, called thermoelectric coefficients while θ is the temperature difference between hot and cold junctions.
The above relation holds for a limited range of temperature. Also the variation of thermo emf drawn against temperature difference between hot and cold junctions is found to be parabolic as shown.
Following experimental setup may be used to the effect of temp. on thermo emf for a given thermocouple:
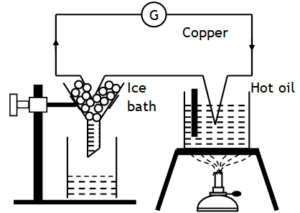
One junction is kept hot by immersing in hot oil bath & the other junction is kept cold by immersing in ice. The temperature of the hot junction can be measured by a thermometer T. The deflection in the sensitive galvanometer G gives a measure of thermo emf.
^Displacement
Suppose a body is moving along a straight line. Let the straight line is along x – axis. Let at a time t1 it was situated at point A at a distance x1 from a fixed point O. Let it moves & at time t2 reaches point B situated at a distance x2 from O.
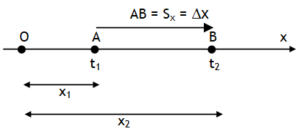
Here the distance AB is called displacement of the body along x axis (Sx) in the time interval t2 – t1 (= Dt). In terms of position coordinates it can be expressed as
Displacement, AB = OB – OA = x2 – x1 or Δx.
i.e. for motion along displacement is equal to the change in position coordinates along that line.
^A long horizontal fixed wire carries a current of 100 A. Directly above and parallel to it is another wire carrying a current of 20 A and weighing 0.04 N/m. The separation between the two wires so that the upper wire is just supported by the magnetic repulsion is