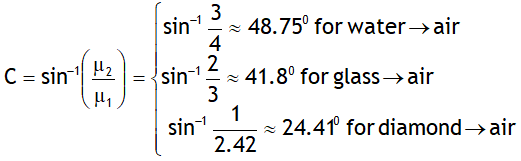^θ without δ
^θ without δ
Under this condition
Such a combination is called a direct vision prism. The required condition is
Posts
^Dispersive power
^Dispersive power
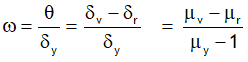
It is independent of A but depends upon nature μmaterial.
From a single prism it is not possible to get deviation without dispersion, or to get dispersion without deviation, however the two or more be combined in such a way that a white ray of light it may undergo:
(a) Dispersion without deviation (i.e. θ without δ)
(b) Deviation without dispersion (i.e. δ without θ)
^Angle of dispersion
θ = δv – δr = [μv – μr] A
^Small angle deviation
^Small angle deviation
δ = A (μ – 1)
δ depends on i, A, μprism, μmedium,
The cause of dispersion is that the speeds of different colours of light in a transparent medium are different.
Also as μv > μr thus δv > δr i.e. the angles of deviation for different colours are different. It is maximum for violet & is minimum for red colour.
^Maximum deviation
^Maximum deviation
A prism shows maximum deviation when incidence angle is maximum i.e. 900, also then
- δmax. = 900 + e – A
- r1 = C
- e = sin–1 [μ sin (A – C)]
^Minimum deviation
^Minimum deviation
If a light ray is incident at an angle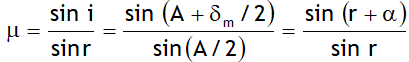 
then it shows minimum deviation, also then
1. 
2. Refracted ray travels parallel to base of the prism if the prism is equilateral
3. δmin. = 2 i – A = 2 i – 2 r = 2 α
4. 
An equilateral prism (i.e. prism angle A = 600) made of ordinary glass (i.e. μ = 1.5) & placed in air (i.e. μ1 = 1), at incidence angle of the 490 shows minimum deviation of 380 with refraction angle of 300.
^Deviation of the emergent ray
^Deviation of the emergent ray
Incident ray deviates clockwise towards the base at first face by amount δ1 (= i1 – r1) & then again deviates clockwise towards the base at second face by amount δ2 (= r2 – i2), thus the total deviation of the prism sum of δ1 & δ2 . Also from the cyclic quadilaternal AEHF,
r1 + i2 = A. From this information we can write
δ = δ1 + δ2 = i1 + r2 – A [Called Prism equation
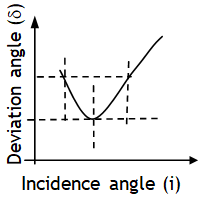
For given μ, λ & A with the increase of incidence angle deviation angle first decreases & becomes minimum & then starts increasing as shown in the graph.
^Prism
^Prism
Prism angle A is also called refracting angle & not angle of refraction.
A light ray DE in incident on the first face AB of a prism ABC at an incidence angle i1. The refracted ray EF bends towards the base BC of the prism has a refraction angle r1 & strikes the second face AC of the prism at an incident angle i2. If i2 < C, then the light ray striking the face AC undergoes refraction & emerges out from the prism as the emergent ray FG.
^Normal shift
^Normal shift
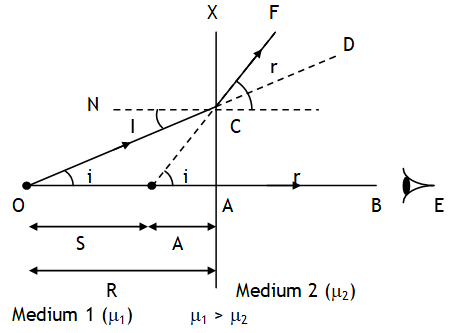
Consider on object O in medium 1 (μ1 > μ2) & observer with eye E in medium 2.
^Critical angle
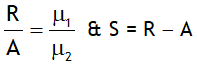
^Critical angle
It is that angle of incidence (i = C) at which a ray going from denser to rare medium shows grazing emergence (r = 900).
