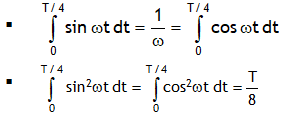Parallel combination of resistors
The voltage is same across each circuit element is same but current is different & is inversely proportional to resistance of that part.
V = V1 = V2 = V3 = I1R1 = I2R2 = I3R3
& 
Fact the maximum number of combination one can have, using all n – resistors at a time is:
(a) 2 (n – 1) [For n – identical resistors
(b) 2n For n – different resistors
Parallel dielectrics in a capacitor
If three dielectric of slabs of same thickness, but different areas of cross section A1, A2 & A3 , dielectric constants K1, K2 & K3 are placed between the plates of a parallel plate capacitor as shown, then the combination behaves as different dielectrics dividing the plate area are considered as capacitors connected parallel.
Capacitance of this is given by
Cnet = C1 + C2 + C3
^What is a Tensor?
A physical quantities which have no specified direction but different values in different directions are called tensors.
Stress, Strain, Density, dielectric constant, refractive index, electrical conductivity, electrical resistivity, moment of inertia etc are tensors. These quantities are taken as tensors at microscopic level & scalars macroscopically.
Following practical units of length are commonly used:
^Uses of dimensions
^Dimensionless Constants
Are the physical quantities which have neither dimensions nor variable values.
e.g. real numbers, e, π etc.
*One steradian
One steradian (sr)is the solid angle subtended at the centre of a sphere by that surface of the sphere which is equal in area to square of the radius of the sphere.
^Standard integrals
Electrostatic field
If the electric field of a charge at a point doesn’t vary with the time, then the electric field is called electrostatic electric field. It’s effect on other charges is studied by defining two quantities; one a scalar field function called electric field potential ‘V’ & second a vector field function called electric field intensity 
are related as
Here the –ve sign implies that electric field intensity due to both positive & negative charged configuration is always in the direction of decreasing field potential i.e. from a region of high potential to a region of low potential.
*Rectangular hyperbola
Function xy = c represents a rectangular hyperbola. It meets both x & y axis at infinity only. It is located in quadrant 1 & 3 if c = +ve & in 2 & 4 if c = – ve.
*Straight line
Function y = m x + c represents a straight line cutting + y at acute angle to +x.
m = tanq is called slope of the line.
q = anticlockwise angle made by the line with + x axis.
m = +ve if line makes acute angle to +x.
m = 0 if line is horizontal.
m = – ve if line makes obtuse angle to +x.
c = +ve if line cuts +y.
c = – ve if line cuts -y.
c = 0 if line passes through origin.
Call 9872662552