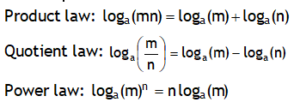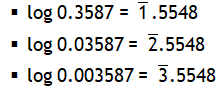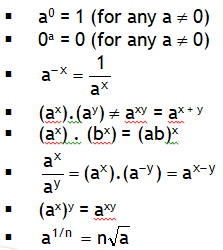^ best physics tuition near me - KP Physics

^Parallel plates with different charges

December 23, 2021/in Back end /by kp-web-admin

Parallel plates with different charges

If the two parallel metal plates X & Y having charge q₁ & q₂ are placed close to each other. Let the medium between the plates is air or vacuum. then in order to make net electric field in each plate zero, charges redistribute such that inner faces have equal & opposite charges & extreme faces have equal & of same sign as shown below

Elec. field on the left side (L) of plates, right side of plate (R) & between the plates due to the charge on face a, b, c & d is

*Principle of homogeneity

December 23, 2021/in Back end /by kp-web-admin

*Principle of homogeneity

According to principle of homogeneity of quantities (PHQ) only those quantities can be added or subtracted which have same physical nature.

e.g. Force can’t be added in velocity, similarly or distance can’t be subtracted from time.

Also according to PHQ: L + L = L and L – L = L

L + T = not possible and T – M = not possible.

However there is no restriction on multiplication or division i.e. quantities having same or different dimensions can be both multiplied as well as divided. e.g. v = x/t, F = m.a, P = F/A, W = F.x etc.

^One radian

December 23, 2021/in Back end /by kp-web-admin

^One radian

One radian (rad) is the angle subtended at the centre of a circle by an arc of length equal to the radius of circle.

^Gaussian surface

December 23, 2021/in Back end /by kp-web-admin

Gaussian surface

To find electric field due to a charge configuration using Gauss’s law we draw an imaginary closed surface around that charged distribution.
Gaussian surfaces are normal to electric lines of & symmetric to the charge enclosed such that electric field at every point of the Gaussian surface due to that charged distribution is same.
Gaussian surfaces are spherical for point charges or spherical distribution of charges & cylindrical for linear and planar distribution of charge.
Only those charges which lie inside the Gaussian surface are considered & that located outside have no contribution in the flux.
Discrete charges on the surface of the -Gaussian surface are not considered (as electric field at the location of a discrete charge is not defined) but continuous charges can be considered.

*Geometrical Meaning of integration

December 23, 2021/in Back end /by kp-web-admin

*Geometrical Meaning of integration

is called Integral or primitive of y w.r.t. x or anti-differentiation.

Here, ydx is area of elementary rectangular strip of thickness dx.

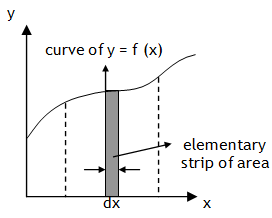
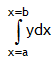Thus gives the total area bounded by the all the elementary strips of the curve represented by the function

y = f (x) with the x-axis between the limits x = a to x = b. As convention upward areas are taken as positive and downward area negative.

^Charge is source of field

December 23, 2021/in Back end /by kp-web-admin

Charge is source of field

An electric charge at rest produces only electric field around it.
An electric charge moving with uniform velocity produces both electric and magnetic fields around it but radiates no energy.
An accelerated charge produces both electric and magnetic fields around it as well as radiates energy in the form of electromagnetic waves.