^Impedance
^Impedance
Net resistance offered by the combination of L, C & R to current in an ac ckt. is called impedance (Z).
Posts
^Current in ac circuits
^Current in ac circuits
Let E = E0 sin ωt is the sinusoidal source of emf applied to a circuit. Let Φ is the phase difference between current & the emf applied is, then the current flowing through the circuit can be represented by the general relation
I = I0 sin (ωt + Φ), its virtual value of current is 
Current flowing in a circuit depends upon following factors:
(a) input voltage signal
(b) frequency of the input voltage signal
(c) nature of circuit elements in the circuit
(d) combination of circuit elements in the circuit
^ac generator
^ac generator
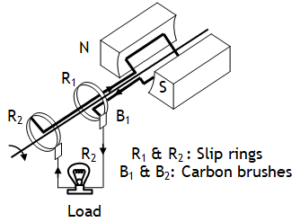
Also called dynamos or electric oscillators or commutators is based on EMI. When a metallic – coil is rotated at a high speed in a strong magnetic field, due to the change in magnetic flux linked with the coil a voltage difference ε = ε0 sin ωt, ε0 = BANω is induced across the two ends of the coil connected to the rings R1 & R2 called Slip rings, which when fed to external load through carbon brushed B1 & B2 can supply current to load.
^Sac (Sinusoidal alternating current)
^Sac (Sinusoidal alternating current)
^LC oscillator or tank circuit
^LC oscillator or tank circuit
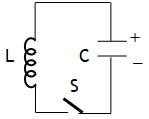
When a charged capacitor is connected to a pure inductor & left for discharging, electromagnetic energy oscillates between capacitor & inductor in due to the sinusoidal variation of charge accordance with the relation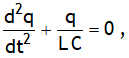 
with q = q0 cosωt & 
.
LC oscillator is equivalent to oscillations of a block connected to a spring on a smooth horizontal surface with following analogy
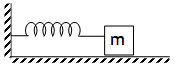
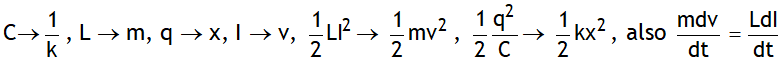
In actual practice the oscillations are damped as every inductor has some resistance.
^Also dimensionally:
^Also dimensionally:
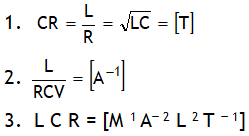
Example of LR circuit
Let at t = 0, switch S is closed.
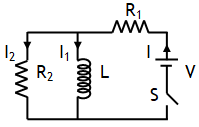
(a) Just on closing switch means t = 0. At this time inductor offers infinite resistance, thus I = 0 and 
(b) A long time after closing switch means at t = ∞. At this time it offers no resistance (as current in inductor attains a maxima), in other words entire current will pass through inductor, hence at t = ∞, I2 = 0 and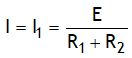 
^Current in LR – circuit
^Current in LR – circuit
An ideal inductor has no ohmic resistance (i.e. R = 0) it has only reactance (i.e. XL ≠ 0). However no inductor is ideal, every inductor can be assumed as series combination of L & R . When such an inductor is connected is connected to a battery (e.g. on throwing switch towards) a current increases exponentially in the outer loop from 0 to become maximum in accordance with the relation 
Due to increase in current voltage across the resistor increases in accordance with the relation 
As the total voltage across the LR combination is always fixed & equal to battery voltage, thus the increase in voltage across the resistor implies a decrease in voltage across the inductor. This is described by the function 
.
On throwing switch towards B current decreases exponentially in the outer loop from maximum to become 0 in accordance with the relation 
^Eddy currents
^Eddy currents
Opposing currents produced in the whole volume of a metallic body in the form of closed loops due to the change in magnetic flux linked with a body oppose the change in magnetic flux & can be so strong that the metallic body become red hot.
^Combination of inductors
^Combination of inductors
^Coefficient of coupling (K)
^Coefficient of coupling (K)
It is defined as, 
(A) The value of K is 0 < K < 1 for loose coupling (i.e. When the axis of two coils are parallel to each other & on different lines )
(B) K = 1 for tight coupling ( i.e. when two coils are wound on each other).
(C) When the axis of two coils are ⊥ to each other & on different lines K = 0 & this case is called zero coupling.
