^One radian
^One radian
One radian (rad) is the angle subtended at the centre of a circle by an arc of length equal to the radius of circle.
Posts
^Gaussian surface
Gaussian surface
- To find electric field due to a charge configuration using Gauss’s law we draw an imaginary closed surface around that charged distribution.
- Gaussian surfaces are normal to electric lines of & symmetric to the charge enclosed such that electric field at every point of the Gaussian surface due to that charged distribution is same.
- Gaussian surfaces are spherical for point charges or spherical distribution of charges & cylindrical for linear and planar distribution of charge.
- Only those charges which lie inside the Gaussian surface are considered & that located outside have no contribution in the flux.
- Discrete charges on the surface of the -Gaussian surface are not considered (as electric field at the location of a discrete charge is not defined) but continuous charges can be considered.
*Geometrical Meaning of integration
*Geometrical Meaning of integration
is called Integral or primitive of y w.r.t. x or anti-differentiation.
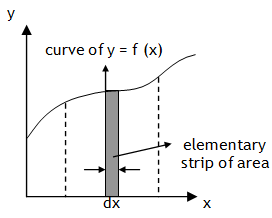
Here, ydx is area of elementary rectangular strip of thickness dx.
Thus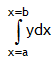 
gives the total area bounded by the all the elementary strips of the curve represented by the function
y = f (x) with the x-axis between the limits x = a to x = b. As convention upward areas are taken as positive and downward area negative.
^Charge is source of field
Charge is source of field
- An electric charge at rest produces only electric field around it.
- An electric charge moving with uniform velocity produces both electric and magnetic fields around it but radiates no energy.
- An accelerated charge produces both electric and magnetic fields around it as well as radiates energy in the form of electromagnetic waves.
*Graph of exponential functions
*Graph of exponential functions
Functions y = ax, a < 1 & y = a– x, a > 1 are exponentially decreasing. Functions y = ax, a > 1 & y = a– x, a<1 are exponentially increasing.
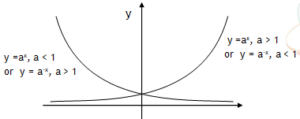
The y intercept of the function y = ax is point (0, 1). If a = e (2.71828) then y = ex is called natural exponential function.
*Right handed or left handed parabola
*Right handed or left handed parabola
A quadratic of the form x = ay2 + by + c represents an right handed or a left handed parabola, it can also be expressed by the following function
(y – v)2 = L (x – u)
Here (u, v) represent coordinates of vertex (V) of a parabola. L= +ve for right handed parabola &
L = – ve for a left handed parabola.
*Trigonometric functions
*Trigonometric functions
We know following values for sinθ & cosθ.
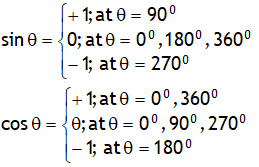
Using these values we can plot the following graphs:
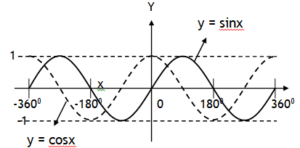
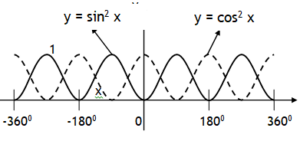
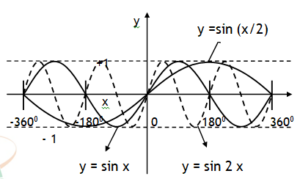
Note the function y = sinx completes one cycle at 3600 where as y = sin2x completes it at 1800 & at
y = sinx/2 completes it at 7200.
*Laws of log
*Laws of log
Examples
- log 3587 = 3.5548
- log 358.7 = 2.5548
- log 35.87 = 1.5548
- log 3.587 = 0.5548
- antilog 0.5220 = 3.327
- antilog 1.5220 = 33.27
- antilog 2.5220 = 332.7
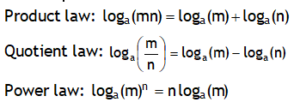
>Laws of exponents
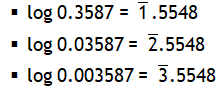
>Laws of exponents
*Harmonic functions
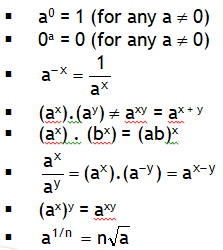
*Harmonic function
Functions which are periodic as well as bounded are called harmonic functions
sinθ & cosθ are harmonic.
