^Ammeter
Ammeter
(a) Constructed by connecting small resistance called shunt (S) in parallel to a galvanometer.
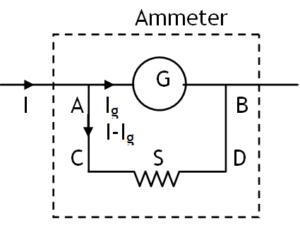
(b) Ig G = (I – Ig) S
(c) 
(d) Used in series with the resistor whose current is to be measured.
Posts
^CR circuits
With switch S thrown towards A, capacitor undergoes charging in accordance with 
With switch S thrown towards B, capacitor undergoes discharging in accordance with 
Here CR = t is called capacitive time constant.
Following table is useful to solve problems based on exponential functions.
^n – cells in series
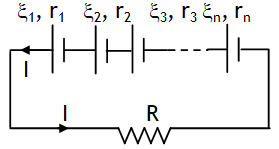
n – cells in series
As all the cell supply current in same direction thus
^Power transferred theorem
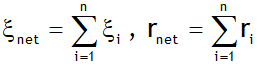
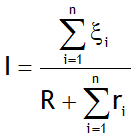
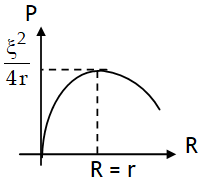
Power transferred theorem
The power transferred by a cell to the load is maximum when R = r & given by
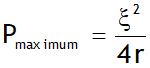
Also then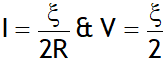 
^Significant figures
^Significant figures
All accurately known digits plus the first uncertain digit of a measurement is called significant digits or significant figures. e.g. if in a measurement, mass of a body lies between 5.6 kg & 5.7 kg & we estimate it as 5.62 kg then the first two digits 5 & 6 are certain while the third digit 2 is approximately known we can say there are 3 significant figures.
Following are the rules for counting significant figures
Rule 1: All non zero digits are significant.
Rule 2: All zeros occuring between two non zero digits are significant.
Rule 3: The digit zero (underlined) conventionally put on the left of a decimal for a number less than one is never significant. All zeros to the right the decimal point are not significant.
Rule 4: The terminal or trailing zero(s) in a number without a decimal point are not significant.
Rule 5: The trailing zero(s) in a number with a decimal point are significant.
Rule 6: The powers of ten are not significant.
Rule 7: No. of significant figures remains unchanged on changing the units of measurement, zeroes appearing in the base number in the scientific notation are significant.
| Example | NSD | Using rule |
| 4567 | Four | 1 |
| 450067 | Six | 2 |
| 0.004567 | Four | 3 |
| 456700 | Four | 4 |
| 0.00456700 | Six | 5 |
| 4.5 x 10 – 6 | Two | 6 |
| 5.300 x 10 6 mm | Four | 7 |
^Series combination of resistors
Series combination of resistors
The current across each circuit element is same, but potential difference is different & proportional to resistance of that part.
i.e. I = I1 = I2 = I3 & V1 = IR1, V2 = IR2, V3 = IR3 & R series = R1 + R2 + R3
^Ohm’s law
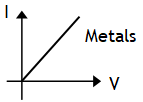
Ohm’s law
(a) 
= constant called electrical resistance R, provided there is no change in the physical conditions like temperature, pressure & impurity etc.
(b) 
= (Microscopic version) i.e. conductivity of a conductor is independent of electric field existing in the material over a wide range of field.
^Energy (potential) stored in a capacitor
Energy (potential) stored in a capacitor
A charged capacitor of any shape or size stores energy (potential) in the form of electrostatic electric field, it is given by
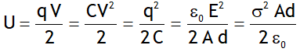
Energy per unit volume is called energy density, it is Electric energy density,
^PPC with a metal slab in plates
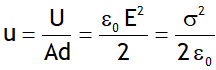
PPC with a metal slab in plates
If a metal slab (dielectric constant K = ∞), thickness t < d is placed between the plates of a PPC, then due to the electric field 
between the capacitor plates the dielectric gets polarized & an electric equal to E0 is induced in it, as a consequence net electric field in dielectric is found to be zero i.e. Enet = 0.
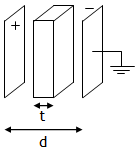
Due to this field electric field net potential difference across the capacitor plates becomes 
Using C = q/V, capacitance of capacitor becomes 
If the conducting slab occupies the entire space available between the plates of capacitor i.e. when t =d & K = ∞, then C = ∞
Comparing (a), (b) & (c) we can say
CDS > CCS > Co
^What is a vector?
^What is a vector?
If both magnitude and direction are required to completely described a physical quantity, then it is called a vector. A vector quantity is represented by putting on arrow above it or by bold letter e.g. it Q is vector then we represent it as or Q. if a quantity can have any direction it is called polar. If its direction is along axis only then called axial.
