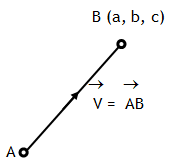
^Mutual induction (M)
1. Property of a coil due to which it suppress the variations in current in it by inducing a back EMF in the neighbouring coil is called mutual induction. It is measured by a quantity called mutual inductance (M), which is defined as, 
.
2. SI unit of both self & mutual inductance is henry (H).
3. For two long coaxial solenoid wound on same core, 
4. Reciprocity theorem: M12 = M21
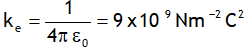
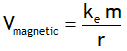
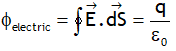
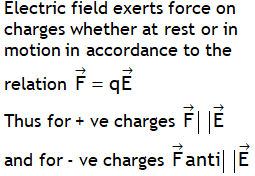
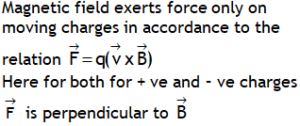
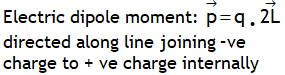
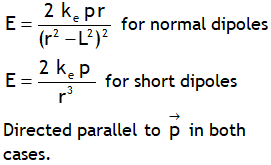
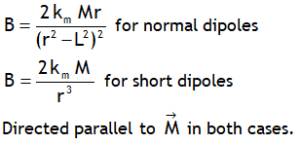
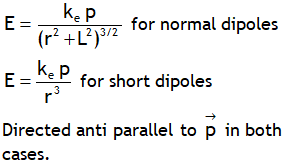
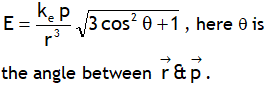
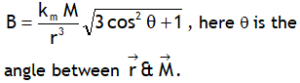
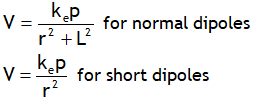
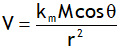
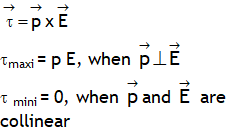
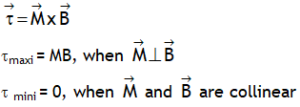
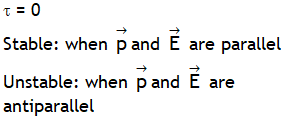
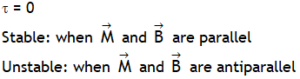
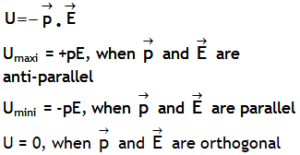
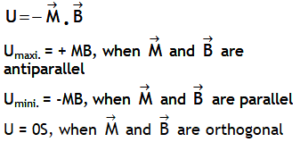
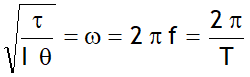
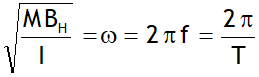
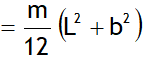
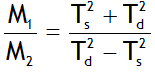
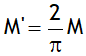^Commonly used results in electricity & magnetism
| Electricity | Magnetism | |
| Source of field | Static or moving charges | Moving charges |
| SI units | Charge: coulomb (C)Electric field: Newton /coulomb (N/C) | Magnetic pole: ampere meter (Am).Magnetic field is tesla (T) |
| Field lines | Discontinuous: Start at a + ve charge & end at equal -ve charge. | Continuous: Have no start or end & are closed loops. |
| Field due to a mono pole |  |
 |
| Proportionality constant | 
(SI units) ke = 1 in cgs units |
 in SI unitskm = 1 in cgs units |
| Force on a monopole |  |
 |
| Potential due to a mono pole |  |
 |
| Coulomb’s law of two point poles |  |
 |
| Screening or shielding | Using hollow metallic boxes. | Using ferromagnetic boxes. |
| Gauss’s law |  |
 |
| Force exerted by field on charge particles |  |
 |
| Trajectories of charged particles in field | In electric field:
1. Straight line if the angle between electric field & velocity of the charges particle is 00 or 1800 & 2. parabolic if the angle between electric field & velocity of the charges particle is other than 00 & 1800. |
In magnetic field:
1. Straight line if the angle between magnetic field & velocity of the charges particle is 00 or 1800, 2. circular if the angle between magnetic field & velocity of the charges particle is 900. 3. helical if the angle between magnetic field & velocity of the charges particle is other than 00, 900 & 1800. |
| Dipole moment of a dipole of length 2 L |  |
 |
| Field on axial line of a dipole |  |
 |
| Field on equatorial of a dipole |  |
 |
| Field at any point of short dipole |  |
 |
| Potential on the axial line of dipole |  |
 |
| Potential at any point of short dipole |  |
 |
| Force on a dipole placed in a region of uniform field | Force on each pole = qE
Net force on dipole = 0 |
Force on each pole = mB
Net force on dipole = 0 |
| Force on a dipole placed in a non uniform field |  |
 |
| Torque acting on dipole placed in a region of uniform field |  |
 |
| Condition for equilibrium of dipole placed in a region of uniform field |  |
 |
| Potential energy of dipole – field system placed in a region of uniform field |  |
 |
^Vibration magnetometer
A magnet free to vibrate about vertical axis passing through its CM is first kept in a non- magnetic hook along BH.
On deflecting it slightly by an amount θ, it experiences a restoring torque due to horizontal component of earth’s field BH
τ = M BH sinθ
≈M BH θ [As sinθ ≈ θ, for small angle deflection.
Due to inertia of the magnet it start oscillating simple harmonically. We know from the theory angular SHM that linear frequency, angular frequency & time period of oscillations is,
Thus for this situation we have
Here, I = MI of the magnet 
Uses:
For two dissimilar magnets using 
Here Ts = time period for the sum position & Td = time period for the difference position.
^Dip circle
Dip circle also called dip needle is a compass pivoted to move about a horizontal axis in a vertical plane containing the magnetic field of the earth i.e. it shows the angle which the magnetic field makes with the vertical. At the magnetic poles such a needle will point straight down.
A compass needle would stay along the magnetic meridian of the place. In some places on the earth there are deposits of magnetic minerals which cause the compass needle to deviate from the magnetic meridian. Knowing the magnetic declination at a place allows us to correct the compass to determine the direction of true north.
^Magnetic meridian
Magnetic meridian at a place is a vertical plane passing through the imaginary line joining the earth’s magnetic north and the south poles or the axis of a freely suspended magnet with its north pole towards geographic north.
^Geographic meridian
Geographic meridian at a point P on earth’s surface is a vertical plane passing through the longitude circle & axis of rotation of the earth.
Properties of a magnet
1. The pole strength ‘m’ of a magnet depends upon the nature of material of a magnet, its state of demagnetization & area of cross section of the magnet but is independent of any bend in the magnet.
2. For a bar magnet 
3. On cutting a magnet in two identical pieces longitudinally (along the length) the pole strength of each part is halved as a result the dipole moment of each part becomes half.
4. On cutting a magnet in two identical pieces transversally (normal to length) the dipole moment of each part becomes as length of each part is halved.
5. A flexible magnet of length L, pole strength m & dipole moment M is bent into a semi circle. The dipole moment of this semicircle will be 
.
6. Demagnetization can be due to heating, hammering, passing AC through an electromagnet, applying demagnetizing field (i.e. a magnetic field in the reverse direction), aging.
Biot–savart’s law
The magnitude of the magnetic field produced depends upon
Direction of magnetic field due to both straight as well as curved conductor can be calculated by right hand stretched thumb rule. For straight conductor thumb point current & curl of fingers point magnetic lines while in a curved conductor reverse of it. On reversing the direction of current the direction of magnetic field produced is reversed.
*Describing a vector
A vector can be expressed as infinite no. of components in 2D or 3 D, however generally a vector is expressed as the resolution of three mutually perpendicular components
a, b & c along x, y & z axis respectively.
Here (a, b, c) are also called direction ratios of 
.
Length of a vector is called its magnitude .. Magnitude of is described as, 
Let makes angle θx, θy & θz with the x, y & z axis respectively. cos of these angels are called direction ratios of & usually expressed in terms of symbols (l, m, n) & are related to direction ratios as
Magnitude of a unit vector is unity i.e.
*Kinematics
Call 9872662552