Conduction
Suppose two charged metal spheres of radii R1 & R2 of different potentials are joined by a metal wire, then charge flows from conductor at higher potential to that at lower potential till both acquire the same potential ‘V’ called common potential. This stage is called steady state & is achieved almost immediately after joining the charged conductors.
1. Common potential at steady state can be calculated using charge conservation i.e. total charge of conductor 1 & 2 before joining
& after joining is same i.e.
q1bj + q2bj = C1 V + C2 V
Or V = V1 aj = V2 aj 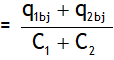
The above relation can be expressed as
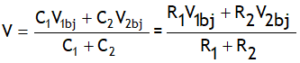
2. Charge on each conductor after joining is
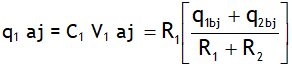
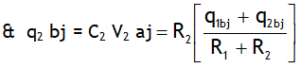
As q = C V & C ∝ R, thus bigger sphere gets more charge after conduction.
3. Total energy of the system before joining is
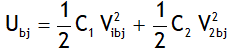
Total energy of the system after joining is
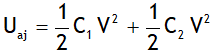
Uaj is found to be smaller than Ubj. The system looses some of its energy in the form of heat, which is given by
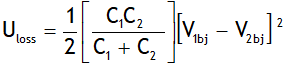

 = constant called electrical resistance R, provided there is no change in the physical conditions like temperature, pressure & impurity etc.
= constant called electrical resistance R, provided there is no change in the physical conditions like temperature, pressure & impurity etc.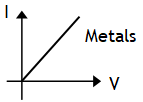
 .
.
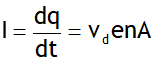
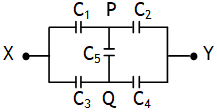
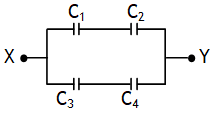
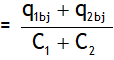
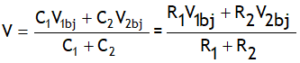
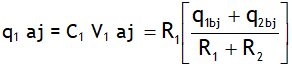
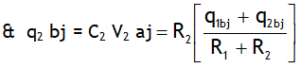
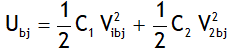
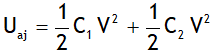
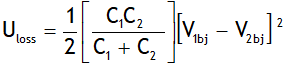
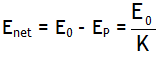 .
.
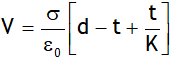 .
.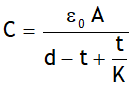 .
.