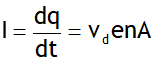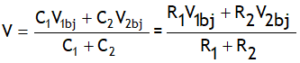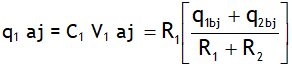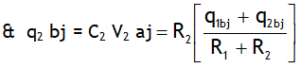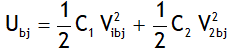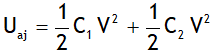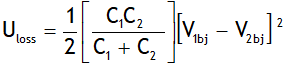Internal resistance

Is the obstruction to the free motion of positive & negative ions of the electrolyte by the viscosity of the electrolyte used in the cell. It is zero for an ideal cell. For a freshly prepared cell the internal resistance is very small & its value increases as the cell is put to more & more use. The internal resistance of a cell varies directly with distance of the electrodes concentration of electrolyte polarisation of the cell & varies inversely varies with the area of electrodes. Both emf & internal resistance are different for different cells & depends on the nature of electrolyte & nature of rods used.

Resistance of a wire on stretching

(a) increases n² times original resistance if length is increased n times.

(b) decreases n⁴ times if the radius of a wire is increased n times.

Provided mass, density & resitivity wire are kept fixed.

Current mechanism in conductors

In metals about 10 ²⁹ m ^{– 3}  of free electrons (called  average number density  ‘n’ ) move randomly (disordered)  in all directions (like motion of gas particles) with average thermal speed of about 10⁵ m/s & collide randomly with the metal ions (almost fixed). Between the collision the free electrons travel along straight lines with average relaxation time (t) of about 10 ^{– 14} s, however due to random motion net charge (electrons) crossing any imaginary plane is zero. On applying external potential difference across a metal an electric field is created in it, which exerts force on electron opposite to the direction of electric field & electron apart from thermal motion (disordered) now start drifting in a definite direction (opposite to the direction of electric field) . Using v – t eqn. the drift velocity of free electrons in metals is .

Average value of drift velocity of free electrons in metals is of the order of few mm /s. Drift velocity per unit applied electric field is called electron mobility (μ) i.e.

Let ‘n’ be the no. density (i.e. N/V) of free electrons of a metal, then current equation for metal slab of cross sectional area A is

1 A is the flow of 6.25 x 10 ¹⁸ electrons per second.