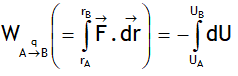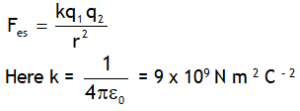^Electric dipole in uniform electric field
Electric dipole in uniform electric field
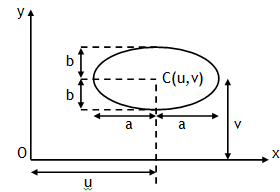
Consider an electric dipole in a region of uniform electric field
1. Net force on the dipole for any position is zero.
2. Torque acting on the dipole is ![]() .
.
3. Torque acts except for the positions when the dipole moment vector & electric field vector are collinear.
4. Total work done by us in rotating the dipole in a uniform electric field is from angle θ1 to θ2 is
W = pE (cos θ1 – cos θ2)
5. The potential energy of an electric dipole placed in a uniform electric field is ![]()
6. A dipole placed in a non uniform electric field experiences both force and torque.
7. Force on a dipole placed in shown non uniform electric field is ![]()
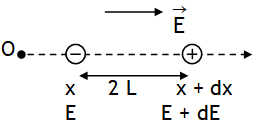

 .
.