^- ve α for electrolytes
– ve α for electrolytes
Cause of decrease in R with increase in temp. for electrolytes is decrease in viscosity.
Posts
^Error in exponential form
^Error in exponential form
Differentiating both sides we can write
The maximum value of fractional error will be
^+ ve α for metals & alloys
+ ve α for metals & alloys
With the increase in temperature of metals & alloys thermal agitation increases & hence the rate of collision increases. As a result the average time t between the successive collision decreases & hence the drift speed decreases, consequently the resistivity of metals increases.
^Resistance of a wire on stretching
Resistance of a wire on stretching
(a) increases n2 times original resistance if length is increased n times.
(b) decreases n4 times if the radius of a wire is increased n times.
Provided mass, density & resitivity wire are kept fixed.
^Resistivity of conductors (ρ)
Resistivity of conductors (ρ)
Resistance per unit length per unit cross sectional area of a material is called its resistivity or specific resistance, for metals it is (a) 
.
Its reciprocal is called conductivity or specific conductance (σ). Both ρ & σ are independent of length, thickness, & shape or geometry.
^Current mechanism in conductors
Current mechanism in conductors
In metals about 10 29 m – 3 of free electrons (called average number density ‘n’ ) move randomly (disordered) in all directions (like motion of gas particles) with average thermal speed of about 105 m/s & collide randomly with the metal ions (almost fixed). Between the collision the free electrons travel along straight lines with average relaxation time (t) of about 10 – 14 s, however due to random motion net charge (electrons) crossing any imaginary plane is zero. On applying external potential difference across a metal an electric field is created in it, which exerts force on electron opposite to the direction of electric field & electron apart from thermal motion (disordered) now start drifting in a definite direction (opposite to the direction of electric field) . Using v – t eqn. the drift velocity of free electrons in metals is 
.
Average value of drift velocity of free electrons in metals is of the order of few mm /s. Drift velocity per unit applied electric field is called electron mobility (μ) i.e.
Let ‘n’ be the no. density (i.e. N/V) of free electrons of a metal, then current equation for metal slab of cross sectional area A is
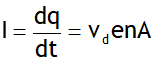
1 A is the flow of 6.25 x 10 18 electrons per second.
^Wheatstone bridge
Wheatstone bridge
The arrangement of five capacitors as shown is called Wheat stone bridge.
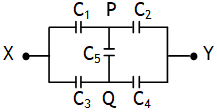
If 
then points P & Q are at same potential & the bridge is said to be balanced, due to this no charge will flow in the arm PQ & hence arm PQ can be removed & circuit can becomes as shown.
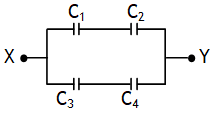
The effective capacitance across the points X & Y for the balanced state of Wheatstone bridge is 
the bridge is not balanced, then the problem can be solved using Kirchoff’s laws.
^Series grouping of capacitors
Series grouping of capacitors
1. Charge on all the components connected in series is same (i.e. q = constant).
2. Potential difference is divided among the various capacitors in accordance with 
e. a capacitor of smaller capacitance will get more potential difference & vice versa.
3. Effective capacitance is given by, 
^Conduction
Conduction
Suppose two charged metal spheres of radii R1 & R2 of different potentials are joined by a metal wire, then charge flows from conductor at higher potential to that at lower potential till both acquire the same potential ‘V’ called common potential. This stage is called steady state & is achieved almost immediately after joining the charged conductors.
1. Common potential at steady state can be calculated using charge conservation i.e. total charge of conductor 1 & 2 before joining
& after joining is same i.e.
q1bj + q2bj = C1 V + C2 V
Or V = V1 aj = V2 aj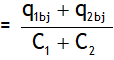 
The above relation can be expressed as
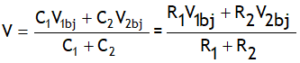
2. Charge on each conductor after joining is
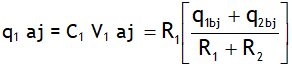
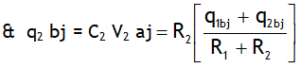
As q = C V & C ∝ R, thus bigger sphere gets more charge after conduction.
3. Total energy of the system before joining is
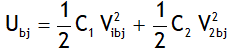
Total energy of the system after joining is
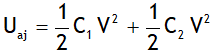
Uaj is found to be smaller than Ubj. The system looses some of its energy in the form of heat, which is given by
^Spherical capacitor outer earthed
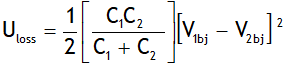
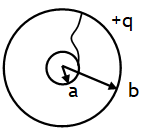
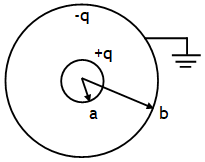
Spherical capacitor outer earthed
Suppose a metal sphere of charge +q & radius a is placed concentrically inside a metal shell of radius b. The charge of a induces charge – q on inner surface & +q on its outer surface of shell b. If shell b is earthed then its +q leaks to earth so that the potential of b becomes zero. Due to earthing & induction the final charge distribution will be
Due to this charge distribution electric field will be
1. E = 0 for r < a (i.e. inside a)
2. 
(radially outward) for a ≤ r ≤ b
3. E = 0 for r > b (i.e. outside b)
Due to this charge distribution the potential on a & b will be
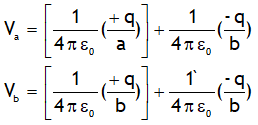
On subtracting above relations we get the potential difference between the a & b, it is
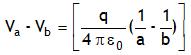
Using C = q/V, capacitance for this system becomes
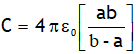
From above result it is clear
1. Let b – a = d is the distance between two spheres & 
, then we can write 
2. in order to have maximum capacitance the radii of two spheres should be as high as possible & separation between them should as small as possible.
3. Suppose the shell b is situated ∞, then we can say sphere a is isolated, then its using b = ∞, we get C = 4 π ε0 a
4. If a & b are very large such that b – a = d & 
, then 
.
5. As 
, thus we can say that the capacitance of a spherical capacitor is always greater than the capacitance of an isolated sphere.
6. If the outer sphere is not earthed & inner sphere is connected to outer by a metallic wire, then entire charge moves outer & capacitance becomes C = 4 π ε0 b.
