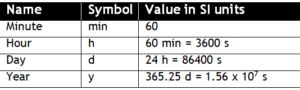
*Value in S.I units
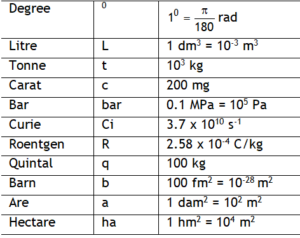
*Value in S.I units
Posts
*Fundamental quantities
*Fundamental quantities
Seven physical quantities have been chosen as fundamental or base quantities these are length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity. Units of base quantities are called base units or fundamental units. Fundamental or base quantities are also known as the seven dimensions of the world.
^Electric flux
Electric flux
1. Electric flux (ΦE) linked with a surface (flat or curved) gives us an idea of the total number of electric field lines passing normally through that surface.
2. Electric flux is defined as the surface integral of the electric field inked with that surface i.e.
Here θ is the angle between electric field vector & area vector (
i.e. an area vector conventionally directed normally outwards to the area under consideration).
3. SI unit of flux: Weber (Wb)
4. CGS unit of flux: Maxwell (Mx)
5. Conversion: 1Wb = 10 8 Maxwell = 1Vm
6. Being dot product, electric flux is a scalar quantity.
7. Maximum value of flux = ± E S
8. Minimum value of flux = 0 (when θ = π/2)
9. If θ is acute flux is + ve & called leaving.
10. If θ is obtuse flux is – ve & called entering.
^Uniformly charged ring of radius R
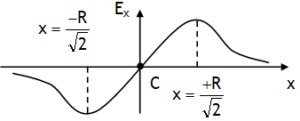
Uniformly charged ring of radius R
1. Charge on a circular ring of radius R & uniform linear charge density λ is, Q = λ 2 πR
2. Electric field on axis at P, 
3. Electric field at centre C = 0
4. 
5. Variation of elec. field vector with distance
6. 
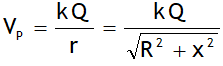
7. 
^Electric dipole in uniform electric field
Electric dipole in uniform electric field
Consider an electric dipole in a region of uniform electric field
1. Net force on the dipole for any position is zero.
2. Torque acting on the dipole is 
.
3. Torque acts except for the positions when the dipole moment vector & electric field vector are collinear.
4. Total work done by us in rotating the dipole in a uniform electric field is from angle θ1 to θ2 is
W = pE (cos θ1 – cos θ2)
5. The potential energy of an electric dipole placed in a uniform electric field is 
6. A dipole placed in a non uniform electric field experiences both force and torque.
7. Force on a dipole placed in shown non uniform electric field is 
^Electrostatic potential (V)
Electrostatic potential (V)
Electrostatic potential energy per unit victim charge is called electrostatic potential i.e. 
using this result & F = q E, LCF can be expressed as 
.
If a charge particle is moved from ∞ → P, then the above relation can be expressed as 
Choice of potential is arbitrary & matter of Convenience, usually we assume V = 0 at infinity.
Bothe field & potential are high when observation point is near a positive charge. Whereas near a negative charge field is high & potential is low.
^Partial derivatives
^Partial derivatives
Let y = f (u, v, w), then ∂y/∂u means partial derivative y w.r.t. u i.e. differentiating y w.r.t. u, keeping v & w constants. Similarly ∂y/∂v means taking partial differentiation of y w.r.t. v, keeping u & w constants.
^Work done by a electrostatic force
Work done by a electrostatic force
Work done by a electrostatic force ‘F’ in moving a point charge ‘q’ from a point A to point a point B situated in conservative electrostatic field
1. is path independent
2. depends only upon the initial & final positions
3. is equal to loss of potential energy of the point charge between these positions. i.e.
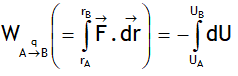
4. zero for a cyclic path.
^Coulomb’s Law
Coulomb’s Law
Force of interaction (attraction or repulsion) between two static point charges is called electrostatic forces. For two static point charges electrostatic forces is described by Coulomb’s law
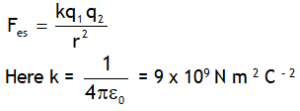
is called electrostatic constant. The quantity eo is called permitivity of free space (vacuum /air). Its value is eo = 8.98755 x 10 –12 N– 1 m – 2 C 2
Dimensions of permittivity: [M – 1 A2 L– 3 T4 ]
Charge which exerts force is called source & which experiences it is called victim.
*Ellipse An ellipse is a closed curve like a circle. An ellipse may be drawn by choosing two points F1 and F2, each of which is a
*Ellipse
An ellipse is a closed curve like a circle. An ellipse may be drawn by choosing two points F1 and F2, each of which is a called a focus, and then drawing a curve through points for which the sum of the distances PF1 and PF2, respectively, is a constant.
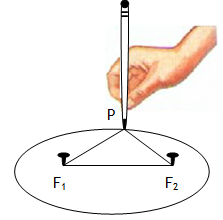
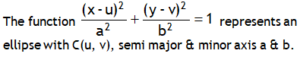
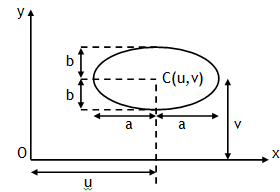
If the center of ellipse is at point origin
Note if a = b, ellipse becomes a circle of radius a.
Area of ellipse = πab
