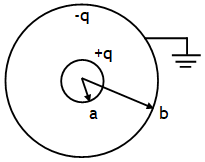
Spherical capacitor outer earthed
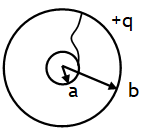
Suppose a metal sphere of charge +q & radius a is placed concentrically inside a metal shell of radius b. The charge of a induces charge – q on inner surface & +q on its outer surface of shell b. If shell b is earthed then its +q leaks to earth so that the potential of b becomes zero. Due to earthing & induction the final charge distribution will be

Due to this charge distribution electric field will be
1. E = 0 for r < a (i.e. inside a)
2. 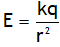 (radially outward) for a ≤ r ≤ b
(radially outward) for a ≤ r ≤ b
3. E = 0 for r > b (i.e. outside b)
Due to this charge distribution the potential on a & b will be
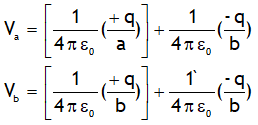
On subtracting above relations we get the potential difference between the a & b, it is
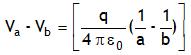
Using C = q/V, capacitance for this system becomes
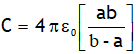
From above result it is clear
1. Let b – a = d is the distance between two spheres & 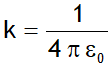 , then we can write
, then we can write 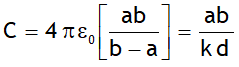
2. in order to have maximum capacitance the radii of two spheres should be as high as possible & separation between them should as small as possible.
3. Suppose the shell b is situated ∞, then we can say sphere a is isolated, then its using b = ∞, we get C = 4 π ε0 a
4. If a & b are very large such that b – a = d & 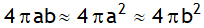 , then
, then 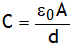 .
.
5. As 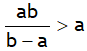 , thus we can say that the capacitance of a spherical capacitor is always greater than the capacitance of an isolated sphere.
, thus we can say that the capacitance of a spherical capacitor is always greater than the capacitance of an isolated sphere.
6. If the outer sphere is not earthed & inner sphere is connected to outer by a metallic wire, then entire charge moves outer & capacitance becomes C = 4 π ε0 b.
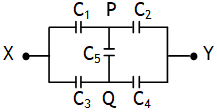
![]() then points P & Q are at same potential & the bridge is said to be balanced, due to this no charge will flow in the arm PQ & hence arm PQ can be removed & circuit can becomes as shown.
then points P & Q are at same potential & the bridge is said to be balanced, due to this no charge will flow in the arm PQ & hence arm PQ can be removed & circuit can becomes as shown.
![]() the bridge is not balanced, then the problem can be solved using Kirchoff’s laws.
the bridge is not balanced, then the problem can be solved using Kirchoff’s laws.
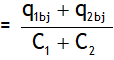
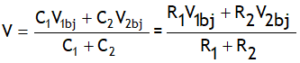
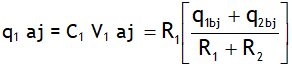
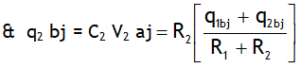
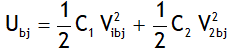
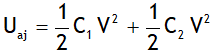
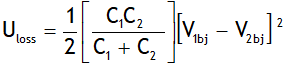


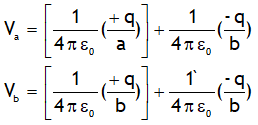
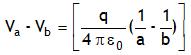
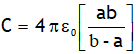

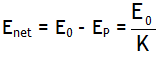 .
.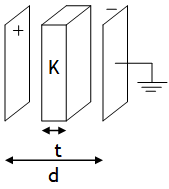
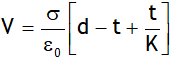 .
.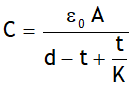 .
.