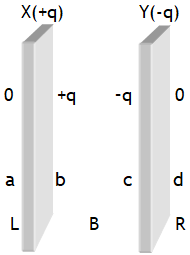
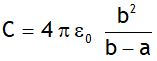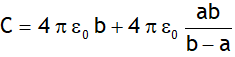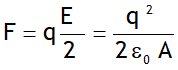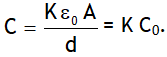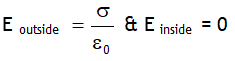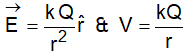Parallel plate capacitor
If the plates X & Y have equal & opposite charges, then charge distribution on plates is as shown in the adjacent drawing. Usually for a parallel plate capacitor we consider this picture.
Let A is the area of each plate, then the charge density of face A, b, c & d are,
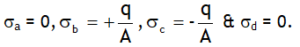
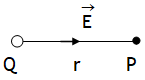
Elec. field on the left side (L) of plates, right side of plate (R) & between the plates due to the charge on face a, b, c & d is
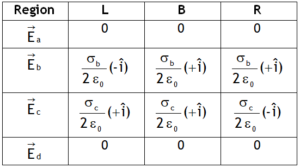
Outside the two plates (i.e. in the regions L & R) the electric field due to the charge on the faces a, b, c & d will cancel out, there will no net electric field outside the plates.
Net elec. field between the plates will be 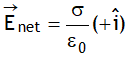
i.e. electric field due to a capacitor plates of equal & opposite charge is zero outside it & inside is 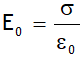 which is uniform both in magnitude & direction, (neglecting fringing). Due to this field there will be attractive force between plates, on each plate it will be,
which is uniform both in magnitude & direction, (neglecting fringing). Due to this field there will be attractive force between plates, on each plate it will be, 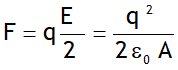
Due to this electric field the potential difference between the plates X & Y separated by distance d is, 
Capacitance of a PPC is

If the entire space is filled with a dielectric, then ε0 → Kε0 & capacitance becomes
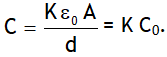
![]()
![]()

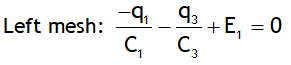
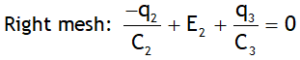
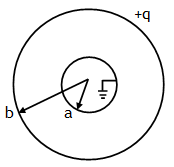


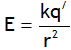 (radially outward) for a ≤ r ≤ b
(radially outward) for a ≤ r ≤ b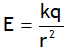 (radially outward) for r > b
(radially outward) for r > b