^Kirchoff’s laws
Kirchoff’s laws
1st or junction rule: ΣI = 0 at any isolated junction to conserve current.
2nd or mesh rule: ΣV = 0 for any closed mesh to conserve energy.
Posts
^Secondary cells
Secondary cells
Secondary cells or accumulators are those which can be recharged. e.g. lead accumulator & alkali cell. Due to smaller internal resistance a secondary cell gives more current than a primary.
^Standard cell
Standard cell
A cell is said to be Standard if its EMF is precisely defined. e.g. Weston – Cadmium cell with an EMF
E = 1.0183 V at 20 0 C.
^EMf of a cell
EMf of a cell
It is defined as the work done by the cell force in moving a unit positive charge inside the cell from the negative to the positive terminal against the potential difference between the cell terminals when no current is drawn from it. i.e. mathematically
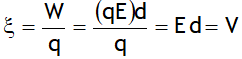
EMF of a cell depends upon Nature & concentration of the electrolyte, temperature of the electrolyte, nature of the electrodes. But is independent of size of electrodes, Distance between the electrodes, area of electrodes immersed in the electrolyte & quantity of electrolyte.
^Zero α for Nichrome, constantan & Manganin
Zero α for Nichrome, constantan & Manganin
i.e. there is appreciably no change (or very slight change) in R with temperature.
1. Constantan (or Eureka) ≡ Cu 60% & Ni 40%
2. Manganin ≡ Cu 84%, Mn 12% & Ni 4%
3. Nichrome ≡ Ni 67.5%, Cr 15%, Fe 16% & Mn 1.5%
^- ve α for semiconductors
– ve α for semiconductors
On heating semiconductors the number density of free electrons increases & τ decreases. But the effect of increase in ‘n’ is stronger than decrease in relaxation time (τ). Hence net effect is increase in ‘n’ which decreases resistance.
^Temperature variation of resistance
Temperature variation of resistance
On heating a material its resistivity changes, which changes the electrical resistance of the material. The electrical resistivity at temperature T can be calculated by using relation: ρT = ρ0 (1+ αT)
^Resistance of various geometries
Resistance of various geometries
Relations 1 to 4 are across length & relations 5 is for radial flow.
Above results are valid for uniform resistivity ρ only.
^The magnitude of the difference between the individual measurement and the actual or true value is called the absolute error in the
^The magnitude of the difference between the individual measurement and the actual or true value is called the absolute error in the
measurement of that quantity. It is represented by 
The ratio of the absolute error to the actual quantity measured is called the relative error of the measurement.
Relative error 
^Continuity equation for Conductors
Continuity equation for Conductors
For a conductor of variable cross section
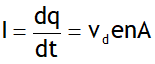
= constant at all sections but drift speed varies inversely with area of cross section.
