^Linear momentum of the EM wave
^Linear momentum of the EM wave
EM waves carry energy and momentum. If a portion of EM wave of energy U propagates with speed c, then linear momentum of the EM wave is 
Posts
^Poynting vector
^Poynting vector
Poynting vector 
gives intensity of EM – wave & is defined as: 
SI unit : W/m2
^Intensity of EM waves
^Intensity of EM waves
Intensity of EM wave is defined as the average energy crossing per second per unit area perpendicular to the direction of propagation of electromagnetic wave. i.e.
^Total energy density of EM waves
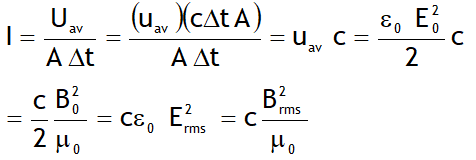
^Total energy density of EM waves
Total energy (u) of EM waves
,
^Magnetic energy density of EM waves
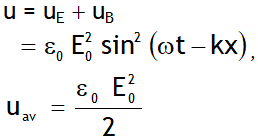
^Magnetic energy density of EM waves
Magnetic energy density (uB) of EM waves is
^Electric energy density of EM waves
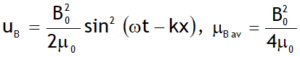
^Electric energy density of EM waves
Electric energy density (uE) of EM waves is
^Speed of EM-waves
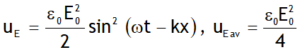
^Speed of EM-waves
Speed of EM wave depends only upon the electric and magnetic properties of medium & is given by
^Equation of EM-waves
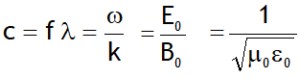
^Equation of EM-waves
For an EM wave propagating along + X-axis is described by the mathematical functions
EY = E0 sin (ωt – kx), EX = 0 & EZ = 0 &
BZ = B0 sin (ωt – kx), BX = 0 & BY = 0
^Propagation of EM-waves
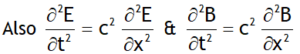
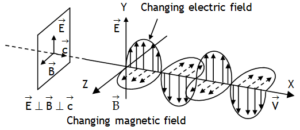
^Propagation of EM-waves
EM waves propagate such that E & B vectors
1. are always in phase
2. vary sinusoidally at right angles to each other as well as it right angles to direction of (DOP) & thus EM waves are transverse.
DOP is in the direction given by 
^Deflection of EMwaves
^Deflection of EM-waves
EM waves are neutral, thus can’t be deflected by E & B fields.
