^Spherical capacitor outer earthed

Spherical capacitor outer earthed

Suppose a metal sphere of charge +q & radius a is placed concentrically inside a metal shell of radius b. The charge of a induces charge – q on inner surface & +q on its outer surface of shell b. If shell b is earthed then its +q leaks to earth so that the potential of b becomes zero. Due to earthing & induction the final charge distribution will be

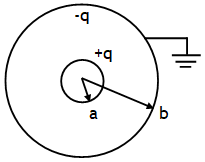
Due to this charge distribution electric field will be

1. E = 0 for r < a (i.e. inside a)

2. (radially outward) for a ≤  r ≤ b

3. E = 0 for r > b (i.e. outside b)

Due to this charge distribution the potential on a & b will be

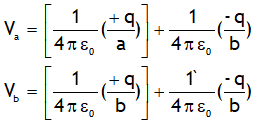
On subtracting above relations we get the potential difference between the a & b, it is

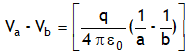
Using C = q/V, capacitance for this system becomes

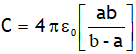
From above result it is clear

1. Let b – a = d is the distance between two spheres & , then we can write

2. in order to have maximum  capacitance the radii of two spheres should be as high as possible & separation between them should as small as possible.

3. Suppose the shell b is situated ∞,  then we can say sphere a is isolated, then its using b = ∞,  we get C = 4 π ε₀ a

4. If a & b are very large such that b – a = d & , then .

5. As , thus we can say that the capacitance of a spherical capacitor is always greater than the capacitance of an isolated sphere.

6. If the outer sphere is not earthed & inner sphere is connected to outer by a metallic wire, then entire charge moves outer & capacitance becomes C = 4 π ε₀ b.