^Comparison of α, β & ϒ rays
^Comparison of α, β & ϒ rays
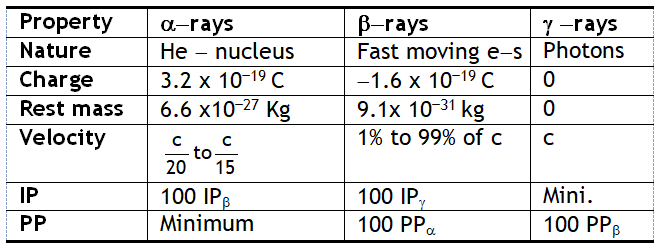
Here IP = Ionizing power & PP = Penetrating power
Also All the three type of rays namely α, β & ϒ affect photographic plate produce flourescence & artificial radioactivity.
^γ-decay
^γ-decay
Most radioisotopes, after an alpha decay or a beta decay, leave the daughter nucleus in an excited state, these excited nuclei make a transition to a state of lower energy by emitting a photon. These photons are charge less, mass less & high energy electromagnetic waves (of the order of million electron volt) & are called the gamma rays.
ZXA (unstable nuclei) → ZXA (stable nuclei) + γ
^Recoil of a gun
^Recoil of a gun
Before firing, both the gun and the bullet are at rest. After firing, the bullet moves with velocity 
and the gun moves with velocity As no external force acts on the system, so using LCLM we get
^Linear momentum conservation
^Linear momentum conservation
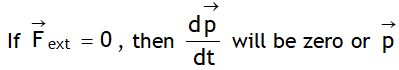
will be a constant , in other words the linear momentum of a system is constant in time if net external force acting on it is zero. LCLM is equivalent to NTL. Consider a two particle system. Let the total linear momentum of the system is not changing with the time i.e. 
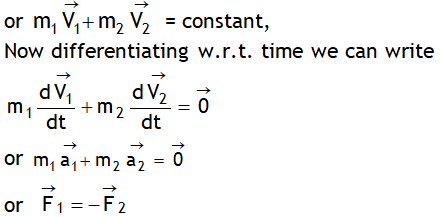
i.e., the two forces i.e. action & reaction are equal & opposite. i.e. for a two particle system the linear momentum of a system will not change with the time only if forces acting on the system are equal & opposite so that net force on the system is zero.
This justifies that LCLM is equivalent to NTL.
^Simple atwood machine
^Simple atwood machine
- NSL for blocks is
System m1: m1g – T = m1a1
System m2: T – m2g T = m2a2
2. Due to inextensible string we have a1 = a2. On adding the two equations we get
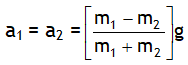
3. Using the value of a in any of the two equations we get
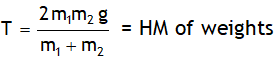
4. From NSL of system pulley we have 2T2 = T/
Thus pull on ceiling is, T/= = 2T
^Block at rest w.r.t . accelerating wedge
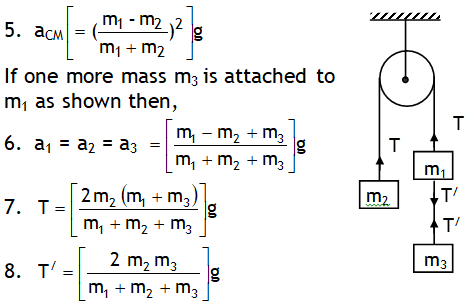
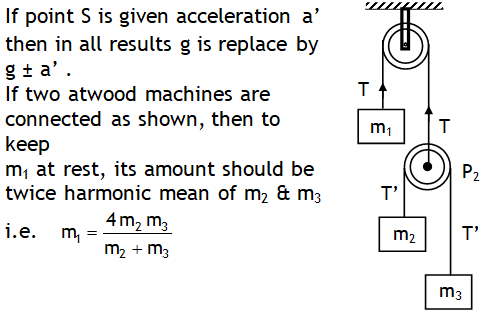
^Block at rest w.r.t . accelerating wedge
Let complete system has acceleration a w.r.t. ground
but the block (mass, m) is to
be kept at rest relative to wedge 
NSL for block + wedge is,
(M + m) a = F
To keep m at rest relative to wedge
ma cosθ = mg sinθ or a = gtanθ
Thus the minimum horizontal force needed should
Be, F = (M + m) g tanθ
Also the normal pressing force exerted by wedge on block is, N = mgcosθ + masinθ = mg secθ
^β-decay
^β-decay
In the beta-minus decay, a neutron inside the nucleus transforms into a proton with the emission of an electron and anti-neutrino are emitted.
Note, the spins of the neutron, proton and electron are all 1/2. In the beta-plus decay, a proton inside the nucleus transforms into a neutron with the emission of a positron and neutrino are emitted.
^α-decay
^α-decay
Consider the following decay
As a nucleus decays due to internal force of repulsion, there is no net external force on it, hence in any nuclear reaction linear momentum must be conserved.
Before disintegration, the nucleus can be assumed to be at rest, so the total momentum was zero. After disintegration let it be mava & mD vD for alpha particle & daughter nuclei respectively. To conserve linear momentum the total vector momentum must still be zero i.e. mava + mDvD = 0 or mava = -mDvD
i.e. momentum of a particle must be equal & opposite to that of daughter’s nucleus.
In magnitude, mava = mDvD
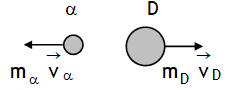
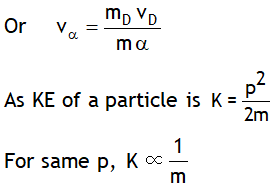
As mass of alpha particle is much lighter than thorium, thus the lighter α particle carries off most of the energy in the form its KE (about 98% of the total KE).
^Radioactivity
^Radioactivity
1. A heavy unstable nucleus (e.g. Uranium, polonium, radium, thorium, actinium, etc.) disintegrates itself naturally, spontaneously & randomly without being forced by any external agent to do so until it acquires stability.
2. The disintegration is independent of all physical and chemical conditions and so it can neither be accelerated nor retarded.
3. The disintegration is random. It is purely a matter of chance for any atom to disintegrate first. It is not possible to predict whether a particular nucleus will decay in a given time interval.
4. The activity (or rate of disintegration, A or R) of a radioactive sample at any instant is directly proportional to the number of undecayed nuclei present in the sample at that instant.
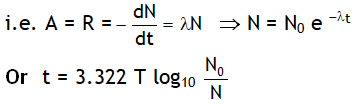
Here λ = disintegration constant or decay constant. & N0 = no. of the atoms present initially i.e. at t = 0.
From above result we can say
- The number of active nuclei in a radioactive sample decreases exponentially with time.
- The disintegration is fast in the beginning but becomes slower and with the passage of time.
- Irrespective of its nature a radioactive sample will take infinitively long time to disintegrate complete.
- The larger the value of decay constant l the higher is the rate of disintegration.
5. Half life (T): 
6. Fraction ‘f’ of substance left undecayed after ‘n’ half lives is given by: 
7. Mean life (τ): 
8. Decay constant (λ) is the reciprocal of time for which 
9. λ = 0 for a stable element (e.g. Pb).
10. (a) 1 Bacqueral (Bq) = 1 d.p.s.
(b) 1 Curie (rd) = 3.7 x 1010 d.p.s.
(c) 1 Rutherford (Rd) = 106 d.p.s.
Here d.p.s. = disintegrations per second.
^Binding energy per nucleon
^Binding energy per nucleon
1. is low for both heavy & light nuclei.
2. increases rapidly up to A = 20 & have peaks for 2He4, 6C12 & 8 O16 .
3. increases gradually after A = 20.
4. becomes less or more flat between A = 40 to 120.
Also it has average value in this region is 8.5 MeV.
5. has maximum value 8.8 MeV for the 26Fe56.
6. decrease after A =120 & drops to 7.6Mev for 92U238.
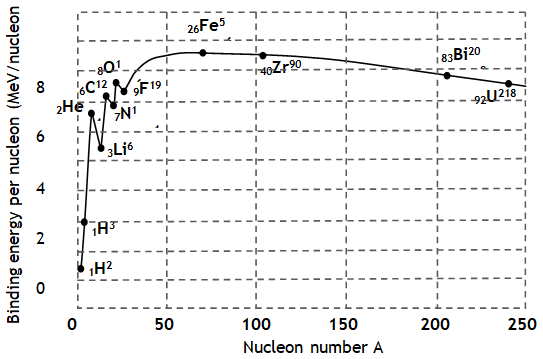
In order to increases the values of binding energies light nuclei undergo fusion while heavy nuclei undergo fission reactions i.e. heavy nuclei become more stable after fission & light nuclei become more stable after fusion.
